Explaining determinants of bank failure prediction via neural additive model

서론
방법론
- 기존의 은행 파산 예측 모델
- Neural Additive Model(NAM) 기반 은행 파산 예측
실험 결과
결론
- 관련 논문

논문명: Explaining determinants of bank failure prediction via neural additive model

저자: Bumho Son, Jaewook Lee, and Hoki Kim

게재지: Applied Economics Letters(2025)

URL: https://www.tandfonline.com/doi/full/10.1080/13504851.2024.2449551

서론

은행의 파산 예측은 금융 안정성을 유지하는 데 필수적이며, 최근 머신 러닝 기법의 발전으로 예측 성능이 크게 향상되었습니다. 그러나 이러한 모델의 블랙박스(black box) 특성은 여전히 중요한 문제로 남아 있습니다. 모델의 내부 작동 방식이 불투명하여 예측 결과를 이해하고 설명하는 데 어려움이 있으며, 이는 금융 분야에서 요구되는 투명성과 책임을 저해합니다.

많은 사후 기법(post-hoc methods)들이 블랙박스 모델의 예측 결과를 설명하기 위해 사용되지만, 이들 기법은 일관된 설명을 제공하지 못하는 한계를 드러내고 있습니다. 이러한 문제는 금융 분야뿐만 아니라 다양한 분야에서 모델 해석의 오류를 초래할 수 있으며, 이는 신뢰성에 대한 의문을 불러일으킵니다. 최근 연구들은 이러한 사후 기법들이 잘못된 설명을 제공할 수 있음을 입증하고 있으며, 이는 예측 결정 요인에 대한 혼란을 초래할 수 있습니다.

“Explaining determinants of bank failure prediction via neural additive model” [Paper]은 이러한 문제를 바탕으로 블랙박스 모델(black box model)과 사후 기법(post-hoc methods)을 활용한 은행 파산 예측에서 발생할 수 있는 위험성을 분석하고자 합니다. 본 연구는 기존 연구에서 도출된 결과를 바탕으로, 사후 기법들(post-hoc methods)이 예측 결정 요인을 일관되게 설명하지 못하는 문제를 지적하고, 이로 인해 발생할 수 있는 모델 해석의 오류를 조명합니다.

본 연구에서 제안하는 Neural Additive Model(NAM)은 강력한 예측 성능을 유지하면서도 해석 가능성(interpretability)을 제공하는 혁신적인 접근법으로, 기존 사후 기법의 한계를 극복하고 예측 성능과 모델의 투명성 간의 균형을 이루는 가능성을 제시합니다. 이는 금융 분야에서 모델 신뢰성을 높이고, 규제 준수를 위한 명확한 설명을 제공하는 데 기여할 것으로 기대됩니다.

방법론

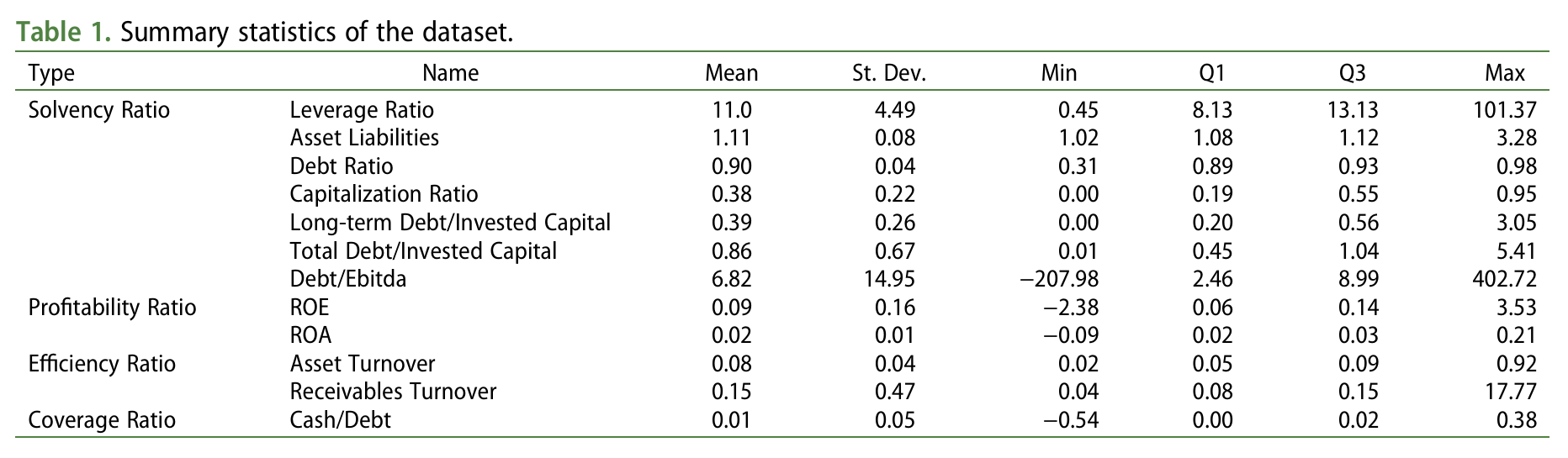
본 연구에서 사용된 데이터는 1969년 1월부터 2021년 9월까지의 기간 동안 뉴욕 증권 거래소(NYSE), 아메리칸 증권 거래소(AMEX), 나스닥에 상장된 21,243개의 은행 데이터를 포함합니다. 각 은행의 주요 변수로는 ROE(자기자본이익률), ROA(자산수익률), 영업수익 대비 영업비용 비율 등이 있습니다. 이 변수들은 건전성(Solvency), 수익성(Profiability), 효율성(Efficiency), 보장 비율(Coverage Ratios) 4가지 범주에 속하는 12개의 널리 사용되는 설명 변수를 기반으로 설정되었습니다. 데이터는 COMPUSTAT에서 수집하였으며, 80%는 훈련 데이터(Train data), 20%는 테스트 데이터(Test data)로 나누어 모델을 학습시켰습니다.

데이터셋 요약 통계

기존의 은행 파산 예측 모델

기존의 은행 파산 예측 모델들은 1970년대 중반까지 고전적인 통계 기법을 사용하여 구축되었습니다. 이후 로지스틱 회귀(logistic regression) 및 의사결정 나무(decision tree)와 같은 머신러닝 방법으로 확장되었고, 최근에는 서포트 벡터 머신(Support Vector Machine, SVM)이나 다중 퍼셉트론(Multi-Layer Perceptron, MLP)과 같은 복잡한 모델이 성능을 더욱 개선하였습니다. 그러나 이러한 복잡한 모델은 설명 가능성(interpretability)이 제한적이라는 문제가 존재합니다.

파산 예측 모델은 은행의 실패 여부를 예측하는 선형 회귀 모델(linear regression model)로 구성됩니다. 모델은 다음과 같은 형태로 나타낼 수 있습니다:

\[\begin{equation} Prob(y_n = 1|x_{n,k}) = \sum_{k=1}^{K} \beta_k x_{n,k} + \alpha \end{equation}\]

여기서 \(K\)는 설명 변수들의 집합을 의미하며, \(Prob(y_n = 1 \mid x_n)\)는 은행 \(n\)에 대한 파산 확률을 나타냅니다.

\[\begin{equation} y_n = \begin{cases} 1 : \text{fail} \\ 0 : \text{non-fail} \end{cases} \end{equation}\]

\(y_n\)은 은행의 파산 여부를 나타내는 목표 변수로, \(y_n\)이 1일 경우 파산(fail), \(y_n\)이 0일 경우 비파산(non-fail)을 의미합니다.

\(x_{n,k}\)는 자산, 수익성 등과 같은 은행 \(n\)의 \(k-\)번째 설명 변수를 나타냅니다.

이 모델의 구조는 선형 회귀 모델(linear regression model)로, 각 설명 변수에 대한 가중치를 곱한 후 합산하는 형태입니다. 로지스틱 회귀(logistic regression)에서는 이 선형 결합을 sigmoid 함수(sigmoid function)를 통해 0과 1 사이의 확률 값을 도출합니다.

해당 수식에서 \(\beta_k\)는 각 설명 변수에 대한 회귀 계수(coefficient)로, 해당 변수가 목표 변수에 미치는 영향을 나타냅니다. 여기서 \(\beta_k>0\)일 경우 파산 확률을 증가시키고, \(\beta_k<0\)일 경우 파산 확률을 감소시키는 것을 의미합니다.

Neural Additive Model(NAM) 기반 은행 파산 예측

따라서 본 연구에서는 Neural Additive Model(NAM)의 구조적 단순성이 제공하는 설명 가능성(explainability)이 선형 회귀(linear regression)의 해석 용이성과 동등한 수준을 유지하면서도, 은행 실패 예측(bank failure prediction) 성능을 혁신적으로 향상시킬 수 있음을 실증합니다. 이 접근법은 복잡한 금융시스템의 블랙박스 문제를 해결하는 동시에 예측 정확도를 확보한 이중적 가치를 지닙니다.

은행 실패 예측 모델링을 다음 두 단계로 공식화합니다:

\[\begin{align} y_n &= f_1(x_{n,1}) + f_2(x_{n,2}) + \cdots + f_K(x_{n,K}) + \alpha \\ &= \sum_{k=1}^{K} f_k(x_{n,k}) + \alpha. \end{align}\]

여기서 각 함수 \(f_k\)는 신경망(Neural Network Architecture)으로 구성됩니다. 각 \(f_k\)는 각 변수에 대해 독립적으로 학습된 함수로 특정 설명 변수 \(x\)에 의존하므로 변수 간의 상호작용이 혼합되지 않아 각 변수의 개별적인 영향을 명확하게 분석할 수 있습니다. 또한 기존의 선형 모델의 기울기가 단순히 가중치로 활용된 것과 달리 각 변수에 대해 복잡한 비선형 변환을 수행할 수 있습니다.

기존 연구(Jo & Kim, 2023; Kraus et al., 2024)에 따르면 Neural Additive Model(NAM)은 시계열을 포함한 다양한 도메인에서 높은 예측 정확도와 설명 가능성을 모두 달성한다는 것이 확인되었습니다. 따라서, 본 연구에서는 Neural Additive Model(NAM)의 구조적 단순성 및 독립된 신경망이라는 특성이 선형 회귀(linear regression)와 유사하면서 설명 가능한 이점 을 제공하면서 은행 파산 예측을 더욱 개선할 수 있다고 가정합니다.

본 연구에서는 로지스틱 회귀(logistic regression), 의사결정 트리(decision tree), 선형 커널(linear kernel) 및 방사형 기저 함수(radial basis function, RBF)를 갖춘 서포트 벡터 머신(Support Vector Machine, SVM), XGBoost, 그리고 다중 퍼셉트론(Multi-Layer Perceptron, MLP)과 같은 다양한 모델을 사용하였습니다. 각 방법은 그리드 검색(grid search)을 통해 하이퍼파라미터 튜닝(hyperparameter tuning) 과정을 거쳤으며, 본 연구의 접근 방식에서는(64, 64, 32) 레이어의 신경망 구조를 채택하였습니다.

모델의 예측 성능 비교(평가 지표에서 가장 좋은 결과 볼드 처리)

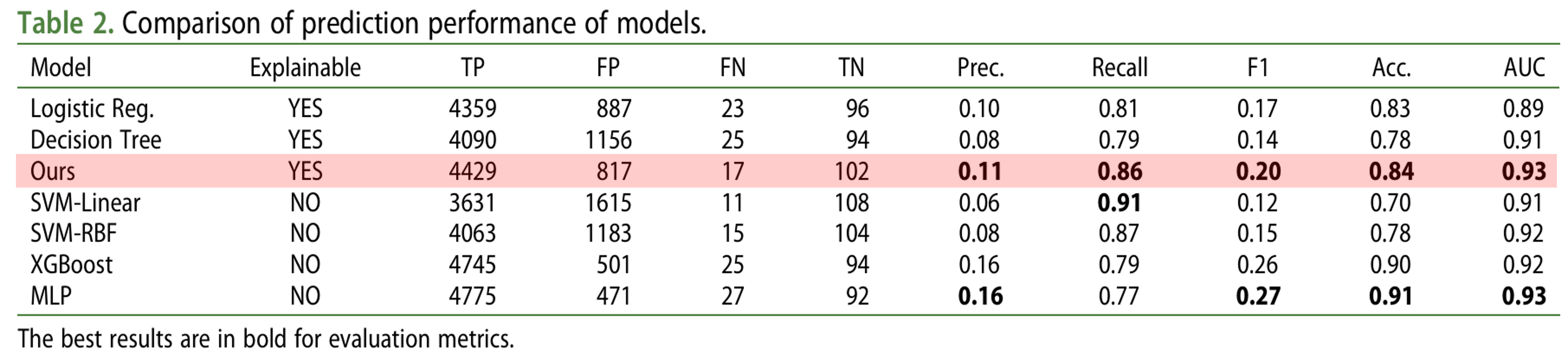
위의 표에서는 정밀도(Precision, Prec.), 재현율(Recall), F1 점수(F1 Score), 정확도(Accuracy, Acc.) 및 AUC(Area Under the Curve)에 대한 결과를 제시합니다. 설명 가능한 모델 중에서 본 연구의 모델(Ours)은 모든 성능 측정에서 로지스틱 회귀(logistic Regression) 및 의사결정 트리(Decision Tree) 모델보다 우수한 성능을 보였습니다. 특히, 본 연구의 모델은 SVM 및 MLP와 같은 다른 비설명 가능한 모델(non-explainable models)과도 유사한 성능을 나타내었습니다.

이러한 결과는 Neural Additive Model(NAM) 기반 접근법이 은행 실패 예측에 있어 설명 가능성(interpretability)과 높은 성능을 동시에 달성할 수 있음을 시사합니다.

실험 결과

다음의 그래프는 각각 서포트 벡터 머신(Support Vector Machine, SVM)과 다층 퍼셉트론(Multi-Layer Perception, MLP) 모델에 사후 분석(post-hoc) 기법인 SHAP(SHapley Additive exPlanations), LIME(Local Interpretable Model-agnostic Explanations)을 적용한 결과와, MLP 모델에 추가로 사후 기법(post-hoc)인 Integrated Gradients(IG)를 적용한 결과를 보여줍니다.

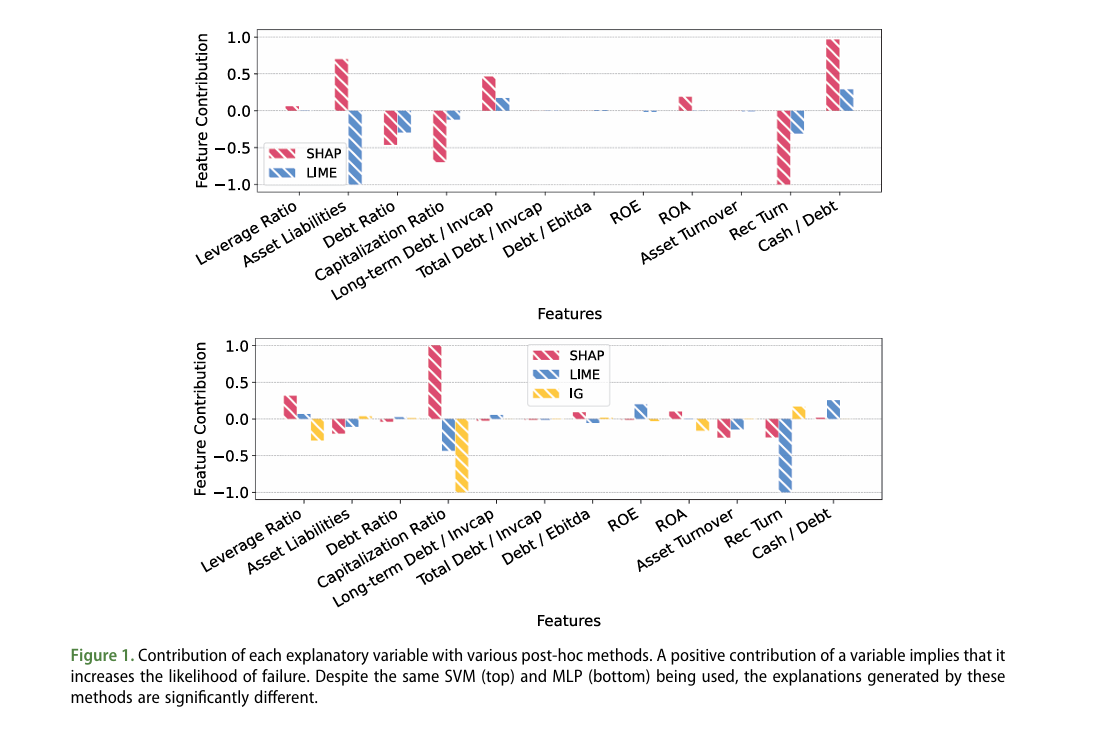
각 설명 변수의 기여도를 다양한 후속 분석 방법을 통해 확인한 결과, 변수의 양의 기여는 실패 확률을 증가시킨다는 것을 의미합니다. 동일한 SVM(상단)과 MLP(하단) 모델을 사용했음에도 불구하고, 이 방법들로 생성된 설명은 크게 다릅니다.

다양한 사후 설명 기법을 통한 각 설명 변수의 기여도

SVM

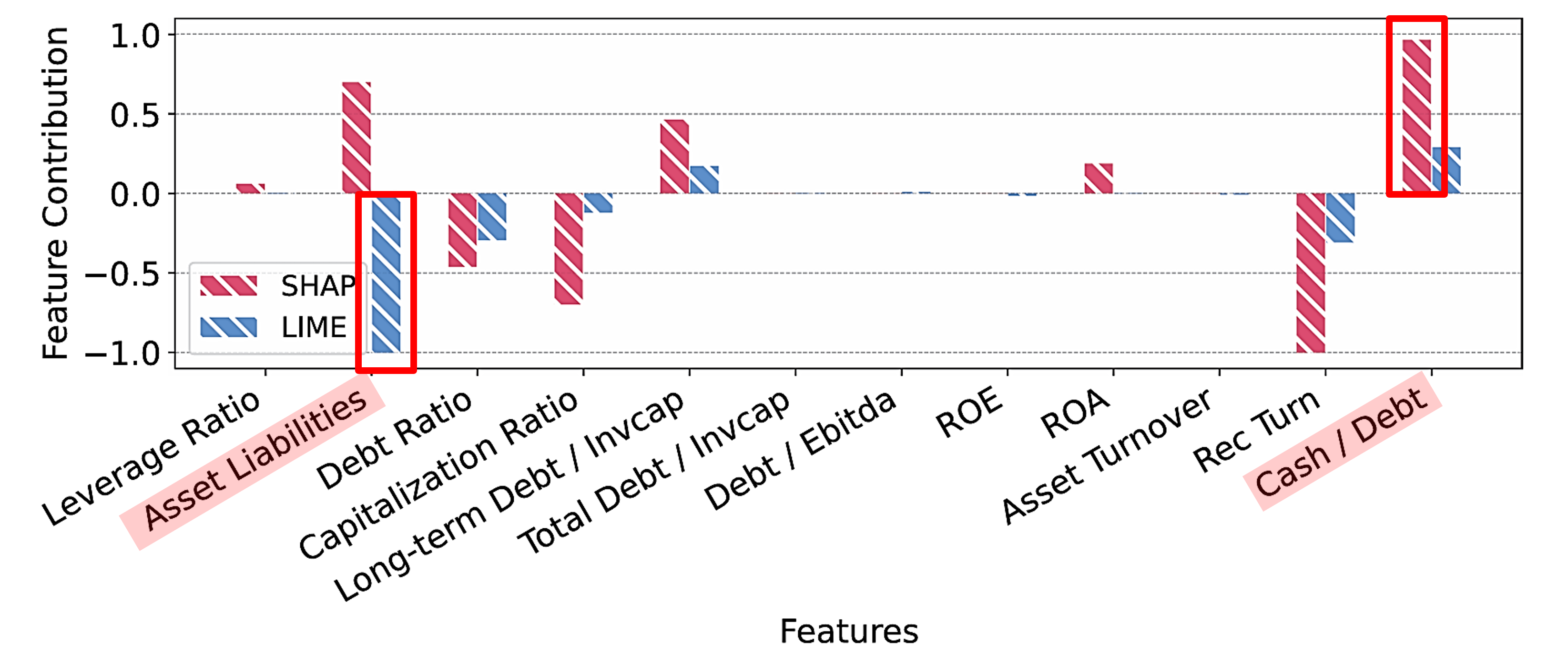
SVM 모델에 SHAP과 LIME 적용(비교를 용이하게 하기 위해 각 특성의 중요도를 −1과 1 사이로 정규화)

서포트 벡터 머신(Support Vector Machine, SVM)에 사후 설명 기법인 SHAP과 LIME을 적용한 결과, 상단 그림에서 SHAP과 LIME은 일관되지 않은 설명을 제공합니다. SHAP은 ‘현금/부채 비율(Cash/Debt)’을 가장 중요한 특성으로 식별한 반면, LIME은 ‘자산/부채 비율(Asset Liabilities)’을 가장 중요한 특성으로 지목합니다.

MLP

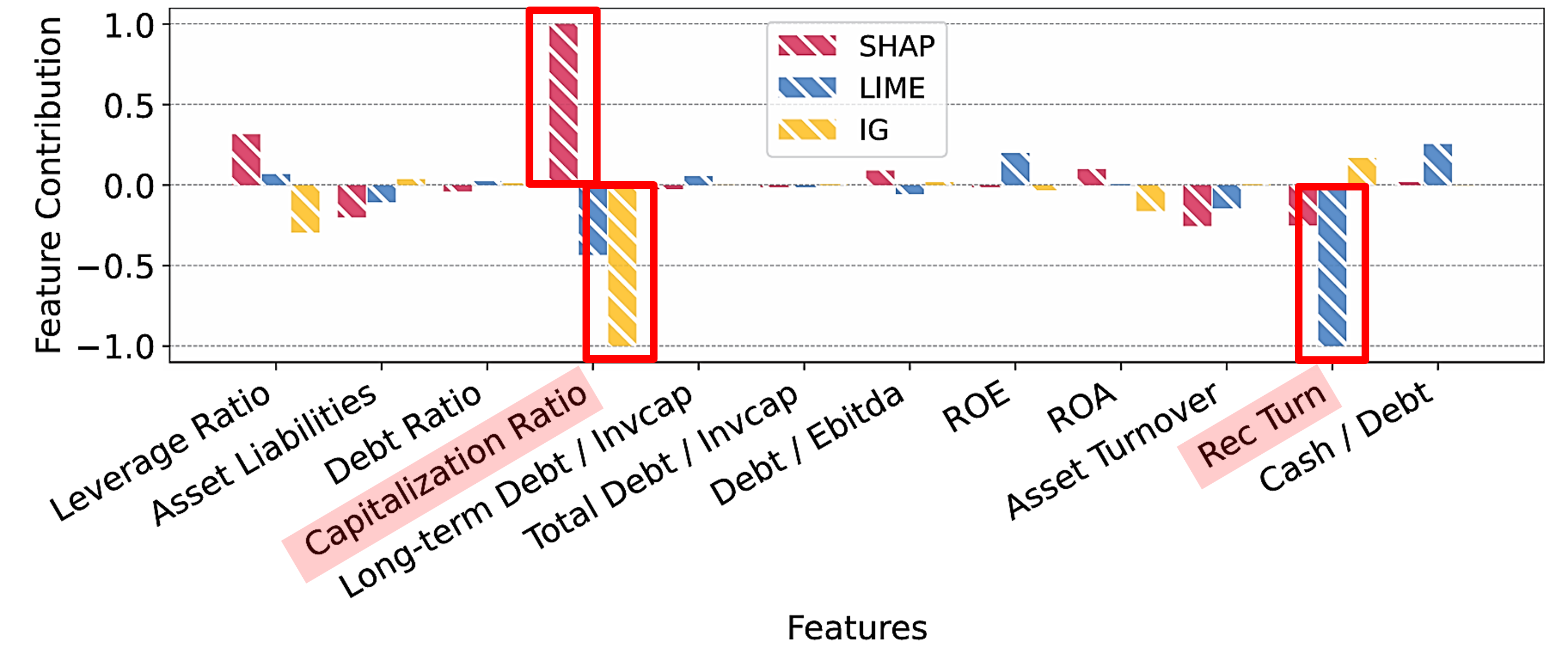
MLP 모델에 SHAP, LIME과 IG 적용(비교를 용이하게 하기 위해 각 특성의 중요도를 −1과 1 사이로 정규화)

다층 퍼셉트론(Multi-Layer Perception, MLP)에서도 유사한 불일치(inconsistencies)가 관찰됩니다. 이러한 일관되지 않은 설명은 금융 분야에서 블랙박스 모델(black-box models)에 사후 기법(post-hoc)을 사용할 때 발생할 수 있는 잠재적인 위험을 강조합니다.

각 설명 변수의 ‘파산(failed)’과 ‘비파산(non-failed)’에 대한 기여도

다음 그래프는 본 연구에서 제안하는 Neural Additive Model(NAM) 기반 모델이 은행의 파산 여부에 따라 각 변수에 부여하는 기여도(contribution)를 시각적으로 나타냅니다. \(y\) 값의 경우, Agarwal et al.(2021)의 연구를 바탕으로, 전체 샘플 \(N\)에 대해 각 변수 \(x_k\)의 기여도는 다음 수식으로 계산됩니다.

\[\begin{equation} f_k(x_k) - \sum_{n=1}^{N} \left( \frac{f_k(x_{n,k})}{N} \right) \end{equation}\]

여기서 \(f_k(x_{n,k})\)는 개별 변수 \(x_k\)가 모델 예측에 미치는 영향을 나타냅니다. 변수의 기여도가 양수(+)일 경우 은행 파산(failed) 가능성을 높이는 요인으로, 음수(-)일 경우 비파산(non-failed) 가능성을 낮추는 요인으로 해석할 수 있습니다.

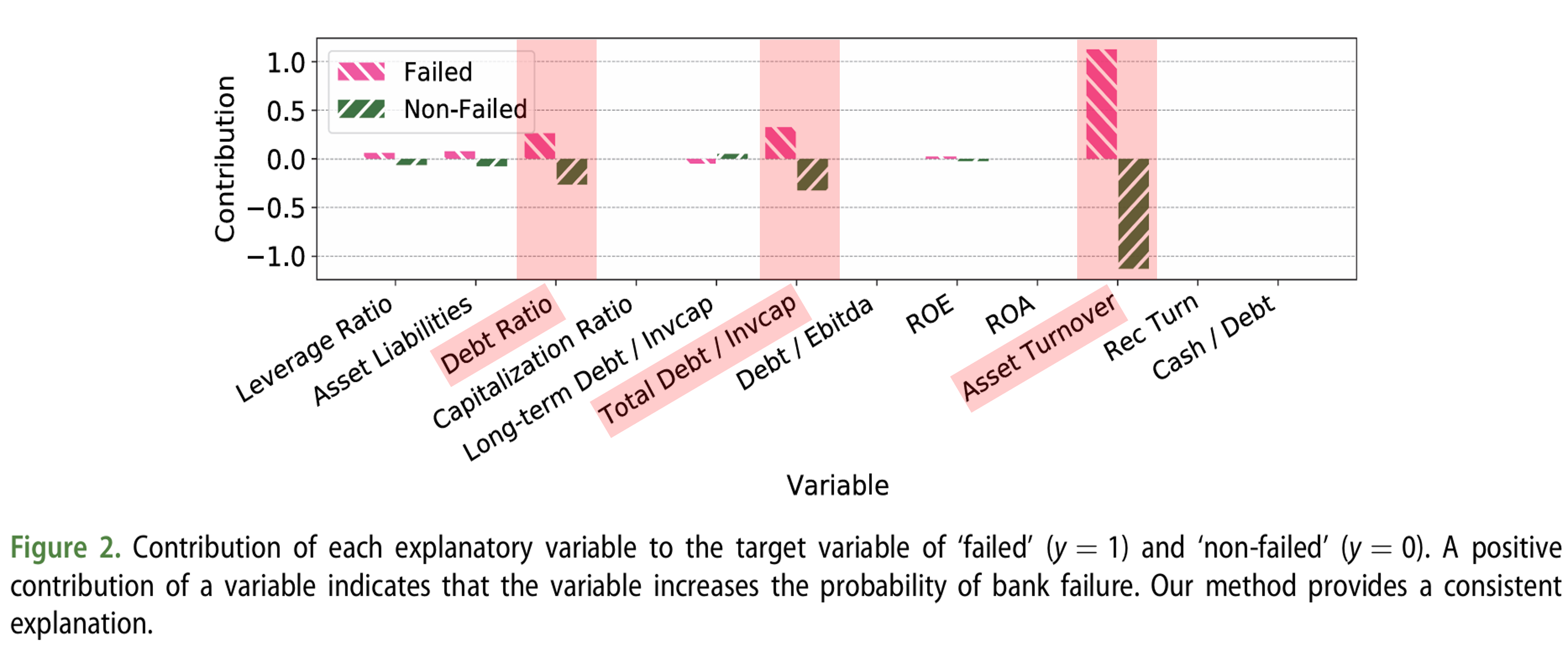
'파산'(y = 1)과 '비파산'(y = 0)에 대한 각 설명 변수의 기여도 변수의 양의 기여는 해당 변수가 은행 파산의 확률을 증가시킨다는 것 의미 NAM(Neural Additive Model)은 일관된 설명 제공(설명가능성이 높다는 것을 의미)

분석 결과, ‘자산 회전율(Asset turnover)’, ‘총 부채/투자 자본(Total-debt /Invcap)’, ‘부채 비율(Debt Ratio)’은 파산(failed) 은행과 비파산(non-failed) 은행 모두에서 높은 기여도를 보였습니다.

먼저 자산 회전율(Asset turnover)의 경우, 기업이 자산을 얼마나 효율적으로 활용하여 매출을 발생시키는지 나타내는 지표입니다. 파산 은행의 경우, 낮은 자산 회전율이 파산 가능성을 높이는 요인으로 작용할 수 있습니다.

다음으로, 총 부채/투자 자본(Total-debt /Invcap)의 경우, 기업의 재무 건전성을 평가하는 지표로, 과도한 부채는 파산 위험을 증가시킬 수 있습니다.

마지막으로, 부채 비율(Debt Ratio)은 총자산 대비 부채의 비율로, 높을수록 재무 위험이 크다는 것을 의미합니다.

이러한 결과는 현금 흐름(cash flow)과 부채 비율(debt ratios)이 파산 예측에 중요한 변수라는 기존 연구 결과(Beaver 1966)와 일치합니다. 즉, 기업의 자산 활용 효율성, 부채 수준, 그리고 전반적인 재무 건전성이 은행 파산 여부를 예측하는 데 중요한 역할을 한다는 것을 시사합니다.

또한, 흥미로운 점은 파산 은행과 비파산 은행 모두에서 ‘자산 회전율(Asset turnover)’, ‘총 부채/투자 자본(Total-debt /Invcap)’, ‘부채 비율(Debt Ratio)’이 높은 기여도를 보였다는 것입니다. 이는 해당 변수들이 은행의 재무 상태를 종합적으로 반영하며, 파산 가능성을 예측하는 데 있어 중요한 지표로 활용될 수 있음을 의미합니다.

중요한 설명 변수 \(x_k\)의 함수 형태 \(f_k(x_k)\)와 고밀도 영역에서의 분포

본 연구에서는 NAM 모델이 은행 파산 예측에 중요하다고 판단한 변수인 ‘자산 회전율(Asset Turnover)’, ‘총 부채/투자 자본(Total Debt/Invested Capital)’, 그리고 ‘부채 비율(Debt Ratio)’의 실제 영향력을 검증하기 위한 분석을 수행했습니다.

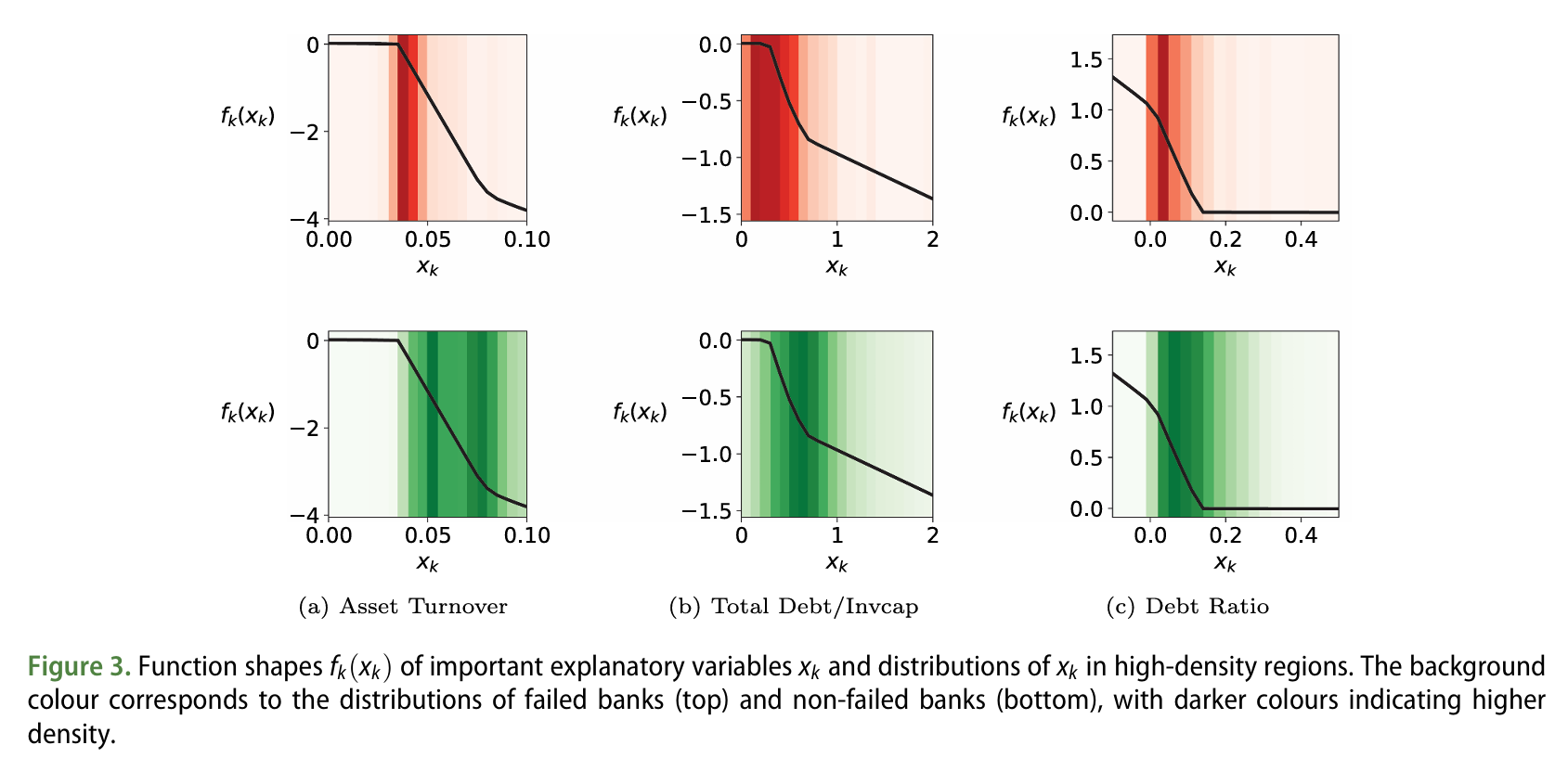
중요한 설명 변수의 함수 형태와 고밀도 지역에서의 분포. 배경 색상은 파산한 은행(상단)과 비파산 은행(하단)의 분포를 나타내며, 어두운 색일수록 밀도가 높음을 의미

해당 그래프는 그림 1에서 식별된 변수들의 함수 형태를 보여줍니다.

(a) 자산 회전율(Asset Turnover)은 낮을수록(0.05 이하) 파산 가능성이 높아지며, 자산을 잘 활용하지 못하는 것을 의미합니다. 자산 회전율이 높을수록 파산 확률이 낮아지고, 실제로 자산 회전율이 높은 비파산 은행의 밀도가 더 높습니다.

(b) 총 부채/투자 자본 비율(Total Debt/Invested Capital)과 (c) 부채 비율(Debt Ratio) 모두 값이 낮을수록 파산 가능성이 높아집니다. 이는 부채가 많을수록 은행의 안정성이 떨어진다는 것을 나타내며, 파산 은행의 밀도가 더 크게 나타납니다.

Neural Additive Model(NAM)은 자산 회전율과 부채 수준 등 중요한 재무 지표들을 바탕으로 파산 가능성을 예측합니다. 이 모델은 기존 연구 결과와 일치하며, 파산 예측에 중요한 변수들을 잘 반영하고 있습니다.

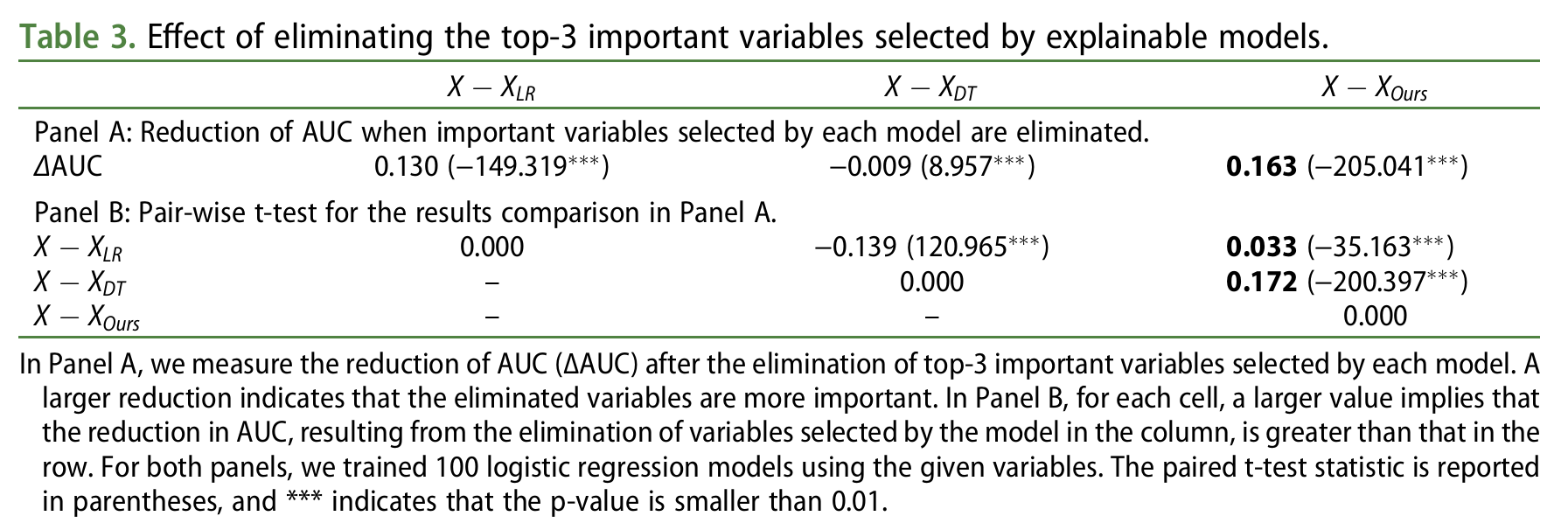
설명 가능한 모델(explainable models)에 의해 선택된 상위 3개의 중요한 변수를 제거한 효과

모델이 식별한 중요한 결정 요인의 정확성을 검증하기 위해, 각 모델에서 상위 3개의 변수를 제거한 후, 100번의 무작위 분할을 통해 로지스틱 회귀 모델을 사용하여 AUC를 측정했습니다. 표 3에 나타난 바와 같이, 우리 모델은 가장 큰 AUC 감소를 보였으며, 이는 다른 모델들보다 중요한 결정 요인을 더 정확하게 식별한다는 것을 의미합니다.

패널 A에서는 각 모델이 선택한 상위 3개의 중요한 변수를 제거한 후, AUC 감소량(∆AUC)을 측정한 결과를 보여줍니다. 감소량이 클수록 해당 변수가 더 중요한 결정 요인임을 나타냅니다. 패널 B에서는 각 셀의 값이 해당 모델이 선택한 변수를 제거한 결과로 인한 AUC 감소가 다른 모델보다 큰지를 비교합니다. 두 패널 모두 100번의 로지스틱 회귀 모델 훈련을 기반으로 했습니다. 쌍체 t-검정 통계량은 괄호 안에 제시되어 있으며, ***는 p-값이 0.01 미만임을 나타냅니다.

결론

본 연구는 은행 파산예측을 위한 블랙박스 모델에서의 사후 설명(post-hoc explanation)의 한계를 다룹니다. 실험을 통해 실증적으로 분석함으로써 Neural Additive Model(NAM)이 예측 성능(predictive performance)을 향상시킬 뿐만 아니라 은행 파산 예측의 중요한 결정 요소들을 신뢰성 있게 제공한다는 것을 확인했습니다. 마지막으로, 각 예측 변수의 역할을 설명하고, 이를 전통적인 은행 파산 예측 분석과 연결시켜 중요한 통찰을 제공합니다.

서론

방법론