논문명: Evaluating practical adversarial robustness of fault diagnosis systems via spectrogram-aware ensemble method
저자: Hoki Kim, Sangho Lee, Jaewook Lee, Woojin Lee, Youngdoo Son
게재지: Engineering Applications of Artificial Intelligence 130(2024)
서론
현대 산업의 복잡성이 증가하면서 생산 효율성이 강화되고 다양한 고객의 요구를 수용할 수 있는 능력이 증대되었습니다. 하지만 베어링 결함 진단 시스템에서 발생하는 문제 역시 같이 증가하고 있어 오작동과 고장을 식별하기 위한 모니터링 시스템이 더욱 중요해지고 있습니다.
데이터 기반 결함 진단 기법은 수집된 데이터를 이용해 학습되며, 시스템 운영 중 발생할 수 있는 미래의 고장을 방지하는 데 사용됩니다. 이때 사용되었던 머신러닝 기법은 미세한 노이즈에 취약하며 이는 곧 적대적 공격(adversarial attack)에 취약하다는 것을 의미합니다. 따라서 결함 진단 모델이 적대적 공격에 얼마나 강건한지 파악하는 것이 매우 중요한 요소입니다.
기존에는 화이트박스(white-box) 모델에서의 적대적 공격이 집중적으로 연구되었으나 실제 모델은 보안상의 이유로 공개되지 않은 블랙박스(black-box) 모델입니다. 즉, 실험 환경이 실제 산업 환경과 맞지 않습니다. 또한, 블랙박스 모델에 대한 적대적 공격 역시 강건성(robustness)을 과대평가하는 문제가 있습니다. 따라서 본 논문은 블랙박스 환경에서 적대적 예제에 spectrogram이라는 도메인 정보를 추가하여 기존 연구에서 발생했던 문제를 해결하고자 합니다.
사전지식
베어링에 대하여
베어링은 inner race, outer race, balls, cage로 구성되며 산업 공학 시스템에서 기본적인 구성 요소로 사용됩니다.
각 구성 요소는 다양한 여러 가지 결함 상태를 포함할 수 있으며 베어링 결함 진단 시스템에는 내륜(inner race) 결함, 외륜(outer race) 결함, 볼(ball) 결함과 정상 상태를 포함하고 있는 CWRU 데이터가 학습 데이터로서 활용되고 있습니다.
베어링 결함 진단 모델은 회전 기계에서의 진동 신호를 input, 기계 상태를 output으로 하며 손실함수로 다음 수식과 같이 크로스 엔트로피를 사용합니다.
\[\begin{equation} \mathcal{L}_{CE}(f(\mathbf{x}), \mathbf{y}) = - \sum_{i=1}^{C} y_i \log(f(\mathbf{x})_i), \quad \text{for } C \text{ classes} \end{equation}\]해당 모델의 목표는 다음과 같은 손실함수를 최소화하는 것입니다.
\[\begin{equation} \arg\min_{f} \mathcal{L}(f(x), y) \end{equation}\]진동 신호 x는 본질적으로 파형의 형태를 띄고 있으며 이전 연구에서 베어링 결함을 보다 효과적으로 진단하기 위해 주파수 도메인의 유용성이 밝혀졌습니다. 특히 베어링 결함이 발생한 경우 주기적인 impulse response가 특정 주파수 대역에서 발생하여 해당 주파수 정보를 활용하여 결함을 정확하게 분석할 수 있습니다. 이때 시간 도메인의 신호를 주파수로 변환하는 방법이 푸리에 변환(Fourier Transform)이며 STFT(Short-Time Fourier Transform)를 통해 푸리에 변환에 시간 정보를 활용하도록 발전하였습니다.
Spectrogram
기존의 FFT는 신호의 전체적인 주파수 성분을 분석할 수 있으나 시간이 지남에 따라 변화하는 주파수 패턴을 포착하는 것이 어렵다는 단점이 있습니다. 이때 spectrogram은 시간에 따른 주파수 변화를 분석할 수 있어 베어링 결함의 특성을 자세히 파악할 수 있습니다. spectrogram을 CNN(Convolutional Neural Network) 모델의 입력으로 사용하여 STFT 기반보다 베어링 결함의 특성을 잘 반영하여 베어링 결함 진단의 정확도를 향상시킬 수 있습니다.
적대적 공격
적대적 공격은 머신러닝을 속이기 위해 악의적인 노이즈 또는 작은 변형(perbutation)을 생성하는 방법입니다. 즉 f가 주어졌을 때 다음과 같은 최적화 문제를 최대화합니다.
\[\begin{equation} d(x; w_u) = D_{KL} \big( p(f(x; w_o)) \parallel p(f(x; w_u)) \big) \end{equation}\]즉, 적대적 공격의 목표는 원래 샘플 x의 정답 라벨 y를 변경하도록 모델을 속이는 것입니다. 많이 알려진 적대적 공격의 예시로는 FGSM(Fast Gradient Sign Method과 PGD(Projected Gradient Descent)가 있습니다.
\[\begin{equation} \delta = \epsilon \cdot \text{sign}(\nabla \mathcal{L}(f(x + \delta), y)) \end{equation}\]FGSM은 다음 수식과 같이 기울기를 이용하여 빠르게 적대적 노이즈를 생성하는 방법으로 손실 함수의 기울기를 따라 단 한 번의 스텝으로 노이즈를 생성하는 기법입니다. PGD는 FGSM의 다중 스텝 버전으로 한 번이 아닌 여러 번 기울기를 업데이트하여 더 강력한 적대적 예제를 생성하는 공격 기법입니다.
\[\begin{equation} \delta(t+1) = \Pi \left[ \delta(t) + \alpha \cdot \text{sign}(\nabla \mathcal{L}(f(x + \delta(t)), y)) \right] \end{equation}\]해당 수식은 t+1번째 스텝에서의 적대적 노이즈를 업데이트하는 과정이며 각 스텝 t에서의 손실함수의 기울기 및 방향을 계산하고 알파만큼 이동하며 노이즈가 엡실론을 초과하지 않도록 수행합니다.
적대적 공격 및 블랙박스 모델
FGSM와 PGD와 같은 간단한 알고리즘을 통해 다양한 분야에서 기계 학습 모델의 성능을 효과적으로 저하시킬 수 있습니다. 특히 베어링 결함 진단 시스템 역시 적대적 공격이 효과적임이 확인되었습니다.
화이트 박스 환경은 공격자가 훈련된 모델에 대한 모든 정보(모델 구조, 가중치, 기울기 정보)를 알고 있다고 가정하는 환경입니다. 하지만 FGSM과 PGD는 결국 손실함수를 기반으로 기울기 정보를 활용하여 공격을 수행해야 하므로 모델 f의 내부 정보를 알아야 효과적으로 수행할 수 있습니다.
따라서 블랙박스 환경에서의 공격을 수행해야 합니다. 일반적으로 훈련된 모델은 공개되지 않는 경우가 더 많으며 특히 산업용 결함 진단 시스템의 경우 모델이 직접 접근 가능한 형태로 제공되지 않으며 IoT 장치를 통해 입력을 제공하는 방식으로만 접근할 수 있습니다.
블랙박스에서의 적대적 공격은 전이 공격(transfer attack)의 방식으로 진행되며 다음과 같습니다.
\[\begin{equation} f(x') \neq y, \quad x' = x + \arg\max \mathcal{L}(g(x + \delta), y) \end{equation}\]이때 g는 소스 모델로 하여 공격자가 접근할 수 있는 공개된 모델 또는 스스로 훈련한 모델이며 특정 회사의 산업용 고장 진단 모델을 목표로 한다면 해당 도메인의 공개된 신경망 모델을 소스 모델로 사용할 수 있습니다.
소스 모델에서 적대적 노이즈를 최적화하여 소스 모델의 손실을 최대화하여 적대적 예제를 생성하여 이를 target model 인 f에 입력합니다.
화이트박스 환경에서는 모델의 강건성을 정확하게 측정할 수 있으나 블랙박스에서는 직접적으로 불가능하므로 1-P(P=공격 성공률)을 근사값으로 사용하였습니다. 하지만 기존의 FGSM, PGD 기법을 단순히 블랙박스 환경에 적용할 경우 실질적인 강건성을 과대평가하게 되어 실제 환경에서 목표 모델이 얼마나 취약한지 정확하게 평가하기 어렵습니다.
도메인 특화 정보를 활용한 적대적 공격
블랙박스 환경에서의 도메인 특화 정보를 반영한 적대적 공격이 효과적이라는 연구가 기존 연구에서 입증되었습니다. 특히 다음 수식과 같이 적대적 예제 최적화 과정에서 공통적인 시각적 변환 T를 적용하면 공격 성능이 향상됩니다.
\[\begin{equation} \max \mathcal{L}(g(T(x + \delta)), y) \end{equation}\]또한 음향 도메인 지식을 활용하여 공격 과정에서 연속적인 노이즈를 추가하면 공격 성능이 향상되는 것을 보입니다.
이처럼 다양한 연구에서 블랙박스 환경의 적대적 공격이 연구되고 있으나 산업용 결함 진단 시스템에서의 블랙박스 환경의 실용적인 강건성을 평가한 연구는 현재 존재하지 않습니다.
따라서 본 논문은 적대적 공격을 최적화하는 과정에서 spectrum 변환을 적용하는 새로운 공격 기법을 제안합니다.
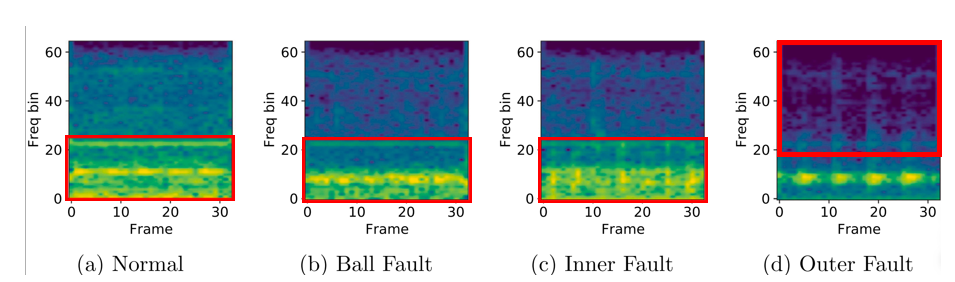
다음 그림과 같이 베어링 결함 진단 시스템에서 spectrum 정보는 강력한 도메인 특성을 제공하며 이를 통해 기존보다 정밀한 모델의 강건성을 평가할 수 있습니다. 본 논문은 블랙박스 환경에서의 적대적 예제 생성 과정에서 spectrum 정보를 조작하는 새로운 정규화 기법을 다음 수식처럼 제안하고 있습니다.
\[\begin{equation} \mathcal{L}_{SC}(x, x^*, \delta) = 1 - \cos(\text{Spec}(x + \delta), \text{Spec}(x)) + \max\left( 0, \cos(\text{Spec}(x + \delta), \text{Spec}(x^*)) - \gamma \right) \end{equation}\]해당 수식은 코사인 임베딩 손실 함수(cosine embedding loss function)로 소스 모델의 노이즈와 원본 모델의 cosine 유사도가 최소가 되며 소스 모델의 노이즈와 목표 모델의 노이즈의 코사인 유사도가 최대가 되도록 최적화합니다. 또한 다음 수식과 같이 크로스 엔트로피와 코사인 임베딩 손실을 결합하여 적대적 노이즈를 업데이트합니다.
\[\begin{equation} \ \delta^{(t+1)} = \Pi_{\|\delta\| \leq \epsilon} \left[ \delta^{(t)} + \alpha \cdot \text{sign} \left( \nabla_{\delta} \left( \mathcal{L}_{CE}(g(x), y) + \beta \mathcal{L}_{SC}(x, x^*, \delta) \right) \right) \right] \ \end{equation}\]Spectrogram 기반 앙상블 기법
spectrogram은 코사인 임베딩 손실에 강한 영향을 미치므로 최적화 과정에서 중요한 역할을 합니다. 본 논문은 추가적으로 윈도우 크기가 적대적 노이즈 생성 성능에 미치는 영향을 추가적으로 분석합니다. 이때 윈도우는 주파수 해상도(frequency resolution)와 시간-주파수 특성 간의 균형을 결정하며 윈도우가 작은 경우 시간 해상도(time resolution)는 높아지나 주파수 정보가 손실되며 윈도우가 큰 경우는 주파수 해상도는 높아지나 시간 정보가 희생되는 트레이드오프가 발생합니다.
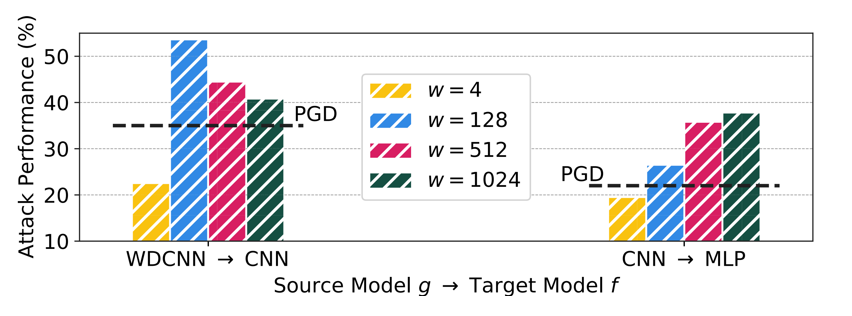
다음 그림은 다양한 윈도우 크기에 따른 소스 모델과 목표 모델 조합의 적대적 공격의 성공률을 분석하였습니다. 윈도우가 너무 작은 경우는 오히려 PGD보다도 낮은 공격 성능을 보이나 소스 모델이 WDCNN(Wide deep Convolutional Neural Network), 목표 모델이 CNN인 경우는 윈도우 크기가 128인 경우가 가장 높은 공격 성능, 소스 모델이 CNN, 목표 모델이 MLP(Multi-layer Perception)인 경우는 윈도우 크기가 1024인 경우가 가장 높은 공격 성능을 보이고 있습니다. 즉, 최적의 w값은 소스 모델과 목표 모델의 조합에 따라 다르다는 것을 알 수 있습니다. 따라서 본 논문은 w값을 단일 값으로 고정하는 것이 아닌 여러 개의 w를 동시에 고려하는 방법을 제안하고 있습니다.
\[\begin{align} \mathcal{L}_{SC}(x, x^*, \delta; w) := 1 & -\cos(\text{Spec}(x + \delta; w), \text{Spec}(x; w)) \\&+ \max \left( 0, \cos(\text{Spec}(x + \delta; w), \text{Spec}(x^*; w)) - \gamma \right) \end{align}\]다음 수식과 같이 spectrogram 정보와 함께 윈도우 정보를 함께 활용하여 각 윈도우 크기에 따라 원본 모델과 소스 모델의 차이를 최대화하면서 목표 모델과의 차이를 최소화하는 방향으로 최적화합니다. 이처럼 다중 윈도우 크기를 활용하는 방식을 통해 본 논문은 SAEM(Spectrogram-aware Ensemble Method)으로 명명하며 코사인 임베딩 손실을 기반으로 도메인 지식을 활용하며 크로스 엔트로피 손실과 결합해 모델을 속이는 최적의 적대적 신호를 생성합니다.
Experiment
본 논문은 실험을 통해 PGD 공격의 한계와 SAEM이 블랙박스 환경에서 뛰어난 공격 성능을 달성한다는 것을 보입니다.
Results
다음 실험은 목표 모델의 조합에 따른 SAEM과 PGD의 공격 성공률을 계산한 실험입니다.
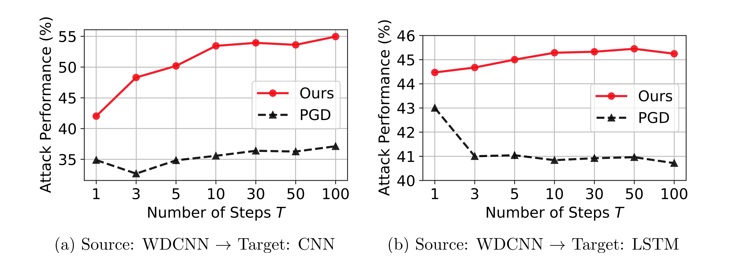
해당 그래프를 보면 SAEM는 스텝 수가 증가함에 따라 공격 성공률이 증가하고 있으며 PGD에 비해 월등히 높은 공격 성공률을 보이고 있습니다.
다음 실험은 PGD와 SAEM으로 생성된 적대적 예제와 원본 예제의 spectrum 정보의 차이가 최대화 되었는지의 여부를 실험하였습니다.
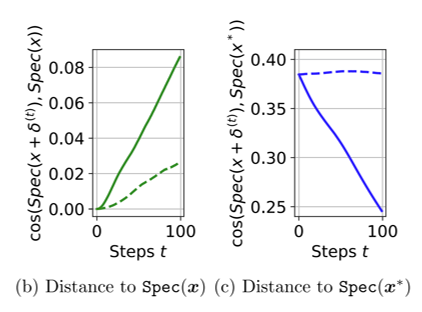
해당 그래프를 보면 SAEM는 적대적 예제와 원본 예제 사이의 spectrum 거리가 더 빠르게 증가하는 모습을 보이며 PGD는 spectrum 정보를 최대화하는데 실패하는 것을 볼 수 있습니다. 또한(c)를 보면 SAEM은 spectrum manifold 상에서 목표 모델과 소스 모델의 거리를 성공적으로 최소화한 것을 볼 수 있습니다.
다음 실험은 Spectrogram 앙상블 조합에 따른 모델의 공격 성능을 비교한 실험입니다.
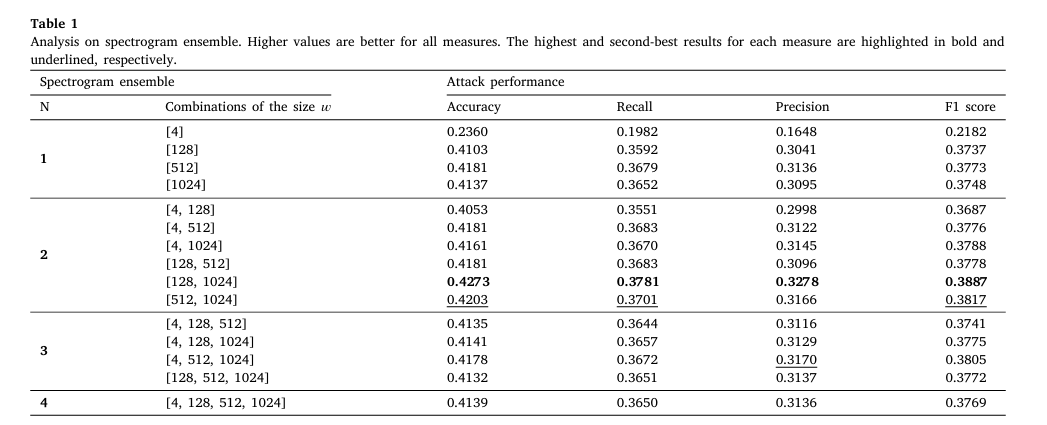
해당 그래프를 보면 w가 [128, 1024] 조합이 가장 높은 공격 성공률을 보이며 평균적으로 작은 윈도우 크기와 큰 윈도우 크기를 결합하는 것이 악의적인 적대적 예제를 생성하는데 유리하다는 것을 알 수 있다.
결론
SAEM은 블랙박스 환경에서 뛰어난 공격 성능을 달성합니다. 추가적으로 산업용 결함 진단 시스템의 실무 환경을 탐색하며 산업 환경에서 발생할 수 있는 잠재적 위험 요소를 식별할 필요가 있습니다. 또한 spectrum 정보를 활용한 방어 메커니즘 연구를 통해서 고장 진단 시스템의 강건성을 향상시키는 연구 및 훈련 데이터셋의 접근성을 포함한 실무 환경에서의 연구가 필요할 것으로 보입니다.