논문명: Neural Network Security: Hiding CNN Parameters with Guided Grad-CAM
저자: Linda Guiga , Andrew William Roscoe
게재지: International Conference on Information Systems Security and Privacy (ICISSP) 2020
서론
CNN(Convolutional Neural Network)은 딥러닝에서 가장 널리 활용되는 신경망 구조 중 하나로, 이미지·영상·음성·텍스트 등 다양한 데이터의 패턴 인식과 특징 추출에서 우수한 성능을 보여줍니다.
그러나 CNN은 널리 사용되는 만큼 다양한 공격의 주요 대상이 되며, 대표적으로 두 가지 공격 유형이 존재합니다.
첫째, 적대적 공격(Adversarial Attack)은 특정 입력에 대해 모델의 출력을 의도적으로 변형하면서도 다른 입력의 출력은 그대로 유지되도록 하는 공격 방식입니다.
둘째, 역공학 공격(Reverse Engineering Attack)은 희생 모델의 핵심 매개변수를 추출하는 것을 목적으로 합니다.
본 연구는 이러한 위협 가운데 특히 역공학 공격에 주목하며, Guided Grad-CAM이라는 시각화 기법을 활용하여 CNN 파라미터 유출을 방지하기 위한 효과적인 방어 방법을 제시합니다.
Background Knowledge
Tramèr는 “Stealing Machine Learning Models via Prediction APIs(2016)”이라는 논문에서 다양한 역공학 공격 기법들을 제시하였습니다.
그 중 대표적인 공격 유형은 방정식 풀이 공격(Equation Solving Attack)과 재학습 공격(Retraining Attack)이 있습니다.
방정식 풀이 공격(Equation Solving Attack)은 모델이 출력하는 확률값을 바탕으로 입력–출력 관계를 방정식으로 세우고 이를 풀어내어 내부 파라미터를 직접 추론하는 방식입니다.
재학습 공격(Retaining Attack)은 모델에 다양한 입력을 질의하여 출력값을 수집한 뒤, 이 데이터로 새로운 모델을 학습시켜 희생 모델의 동작을 모방하는 방식입니다.
Retraining Attack은 Eqeuatino Solving Attack과 비교했을 때 훨씬 더 많은 쿼리 예산을 필요로 합니다.
따라서 본 연구에서는 공격의 타겟으로 설정한 모델인 CNN의 파라미터 수가 매우 많다는 점과 confidence 값 활용 가능성을 고려하여Equation Solving Attack을 공격 기법으로 선정하고 그에 맞는 방어 기법을 제안합니다.
본론
이 논문에서 제시하고 있는 CNN 모델의 파라미터 보호를 위해 사용되는 방어 기법은 입력값에 노이즈를 추가하는 방법입니다.
이를 통해 모델의 성능은 유지하면서 내부 파라미터 값을 추출하기 힘들도록 만듭니다.
노이즈는 Guided Grad-CAM이라는 시각화 기법을 활용하여 이미지의 특정 픽셀값에 추가됩니다.
Guided Grad-CAM
CNN의 뉴런들은 각각 예측에 영향을 미치는 정도가 다릅니다. 일부 연구(Mahendran & Vedaldi, 2016)에서는 CNN의 마지막 계층이 이미지의 전역적 특징(Global Characteristics)을 더 많이 반영한다는 점을 발견하였습니다.
따라서 마지막 합성곱 계층의 뉴런을 분석하면, 모델이 예측 시 어떤 부분을 가장 중요하게 활용하는지를 파악할 수 있습니다. 이러한 배경에서 Selvaraju et al.(2016)은 Guided Grad-CAM 기법을 제안하였습니다.
Guided Grad-CAM은 마지막 합성곱 계층의 기울기(Gradient)를 기반으로 시각적 설명 맵을 생성하여, 모델이 입력 이미지의 어느 영역에 주목했는지를 보여줌으로써 CNN 모델의 설명가능성(Explainability)을 높여줍니다.
Guided Grad-CAM은 이름에서도 알 수 있듯이, Guided Backpropagation과 Grad-CAM을 결합한 방법입니다. Guided Backpropagation은 픽셀 단위의 세밀한 정보를 제공하는 반면, Grad-CAM은 클래스별로 의미 있는 특징 영역을 강조합니다.

위 그림은 개와 고양이가 같이 있는 이미지에서 개의 대한 예측과 고양이에 대한 예측에서의 의미 있는 특징 영역들을 각각의 시각화 기법으로 나타냈을 때의 결과를 보여줍니다.
Proposed Method
본 연구에서는 Guided Grad-CAM을 활용하여 모델이 이미지의 클래스를 예측할 때, 입력 이미지에서 노이즈를 추가할 픽셀을 선정하여 노이즈를 추가하는 방법을 제안합니다. 이를 통해 CNN 모델의 파라미터(가중치)를 추출하기 어렵게 만듭니다.
공격자의 입력 쿼리를 $ x $라고 할 때, 노이즈 $ n $이 입력값에 더해져 출력값 $f(x’)$를 얻도록 유도합니다$ (x’ = x+n)$.
노이즈를 추가할 픽셀을 선정할 때, Guided Grad-CAM을 활용하여 중요도가 낮은 픽셀을 선정합니다. 왜냐하면 노이즈 추가는 모델의 예측값을 바꾸지 않으면서 가중치 추출이 어렵도록 이루어져야 하기 때문입니다. 이 때 중요하지 않은 모델을 선정하는 기준치(threshold)는 $ t $로 표현됩니다.
우리가 주입하는 노이즈 $n$는 선택된 픽셀 집합 $S$ 위에서 정의된 정규분포 \(\mathcal{N}(\mu,\ \sigma^2)\)를 따릅니다. 여기서 $ \mu $(평균)가 크면 선형 연산을 거치며 출력이 전반적으로 치우쳐 노이즈 성분이 강하게 드러나고, $ \sigma $(표준편차)가 크면 노이즈의 변동성이 커지고 모델이 원래 입력값에 덜 의존하게 됩니다. 이때 모델 내부의 배치 정규화(Batch Normalization)이 입력 분포의 급격한 변화를 제한해 학습의 안정성과 성능을 유지하도록 돕습니다.
\[\tilde{x}_{i,j}=\frac{x_{i,j}-\mu_{\text{batch}}}{\sqrt{V_{\text{batch}}+\varepsilon}}\]Experiment
본 연구의 실험에서는 공격자가 공격의 타겟이 되는 모델의 아키텍처를 추정할 수 있고, 입력 쿼리 수는 제한이 없다고 가정합니다.
먼저 $ t $의 값에 따라 얼마나 많은 픽셀들에 노이즈가 삽입되고, 정확도가 변화하는지 측정하였습니다.
- 모델 아키텍처 : VGG-19
- 데이터셋 : IMAGENET
- $ p $ = Guided-Grad-CAM 맵의 해당 픽셀 값
- $m$ = Guided-Grad-CAM 맵의 최댓값
- $t$ = 기준치(threshold)
$ t $값에 따라 노이즈를 삽입할 픽셀들을 선택하고, $ \mu$ = 125, $\sigma$ = 25인 정규분포를 따르는 노이즈를 삽입한 결과는 다음 이미지와 같았습니다.
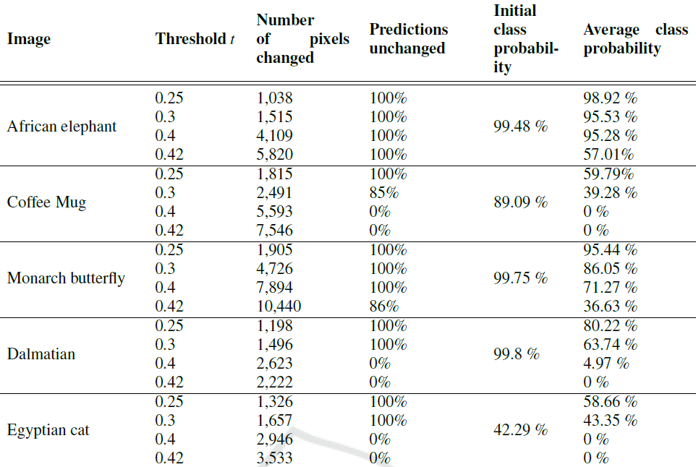
결과를 보면, $t$값이 증가함에 따라 노이즈가 삽입된 픽셀의 개수가 커지고, 모델의 예측이 변화한 정도가 클래스별로 각각 달라집니다. 모델의 5개 클래스 예측 결과가 모두 달라지지 않는 $t$의 최댓값은 0.25였고, 따라서 앞으로의 실험에서 threshold 값은 0.25를 기본으로 설정하였습니다.

위 실험을 통해 $ t = 0.25$ 일 때 최적의 방어가 이루어짐을 확인하였고, 이를 최초의 CNN 모델인 LeNet에 적용시켰습니다.
실험 환경 설정은 다음과 같습니다.
- 모델 : LeNet(오리지널 버전 및 배치 정규화 계층 추가 버전)
- 데이터셋 : CIFAR-10
- 추가하는 노이즈의 평균과 표준편차 $\mu = 0.8, $ $\sigma = 0.1$
위와 같은 설정으로 첫 번째는 (a)모델에 방어 기법을 적용하였을 때 방어 기법을 적용하기 전과 비교하여 얼마나 성능이 달라지는지 평가하고, 두 번째로 (b)배치 정규화를 첫 번째 Convolution layer에 추가한 후 방어 기법 적용 모델의 성능을 평가하고, 이후 (c)방어 기법 적용된 모델로 공격자가 추출 모델을 만들었을 때 얼마나 성능이 떨어지는지 평가하였습니다.
결과:
- (a)의 결과 방어 기법을 적용한 모델에서 전체 픽셀의 2%가 중요하지 않은 픽셀로 선정되어 노이즈가 추가되었고, 원본 모델과의 예측 일치율은 82%였습니다.
- 픽셀을 선정하지 않고 이미지 전체에 노이즈를 삽입했을 때의 정확도는 79.8%로, Guided Grad-CAM을 활용하는 것이 더 효율적임을 확인했습니다.
- (b)의 결과 전체 픽셀의 1.8%에 노이즈가 추가되었고, 원본 모델과의 예측 일치율은 89.5%였습니다.
(c)를 실험하기 위해서 먼저 공격자가 추출 모델을 만든 방법은 Tramer가 제시한 Equation Solving Attack으로 선정하였습니다. 공격 대상은 LeNet Architecture의 마지막 layer로 설정하였습니다. 공격 성능 평가 지표는 다음과 같은 수식을 사용했습니다.
\[E(f,\tilde{f}) \;=\; \sum_{x \in D} \frac{ d\!\left(f(x),\, \tilde{f}(x)\right) }{|D|}\] \[E_{\mathrm{var}}(f,\tilde{f}) \;=\; \sum_{x \in D} \frac{ d_{\mathrm{var}}\!\left(f(x),\, \tilde{f}(x)\right) }{|D|}\] \[d_{\mathrm{var}}\!\big(f(x),\tilde f(x)\big) = \frac12 \sum_{i=1}^{c} \left|\, p_i - q_i \,\right|.\]$ f,\tilde{f} $ 는 각각 피해 모델과 공격자의 추출 모델이며, $D$는 테스트 데이터셋을 나타냅니다. $d$는 두 모델의 예측 레이블이 같은지만 보는 distance로 같으면 0, 다르면 1로 정의됩니다. $d_{\mathrm{var}}$는 두 모델이 확률분포의 차이를 재는 총 변동 분포입니다.
LeNet 모델 대상으로 마지막 layer에 공격을 수행할 때, 원본 LeNet 모델과 첫 convolution layer의 필터를 16개에서 6개로 줄인 단순화한 LeNet 모델 모두를 대상으로 공격을 수행하였습니다. 이 때, 원본 모델과의 유사도는 $ 1-E, 1- E_{\mathrm{var}}$ 로 측정하였습니다.
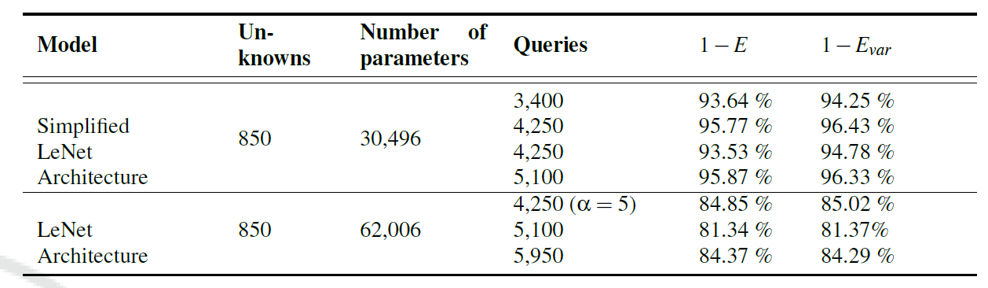
LeNet을 단순화 한 것은 파라미터 개수 등 실험의 효율성을 위함이었고, 이 실험의 결과로 알 수 있던 것은 앞단 표현이 단순할수록 마지막 층 가중치 추출이 훨씬 쉬워진다는 점을 보여줍니다.
(c)를 위 공격 방법을 적용하고 실험하였습니다. 이 때, 배치 정규화를 포함한 모델과 포함하지 않은 모델의 결과도 비교하였습니다.
각각의 모델에 대한 원본 모델의 CIFAR-10 테스트 셋 데이터에 대한 정확도는 64.6%와 62.7% 였습니다.
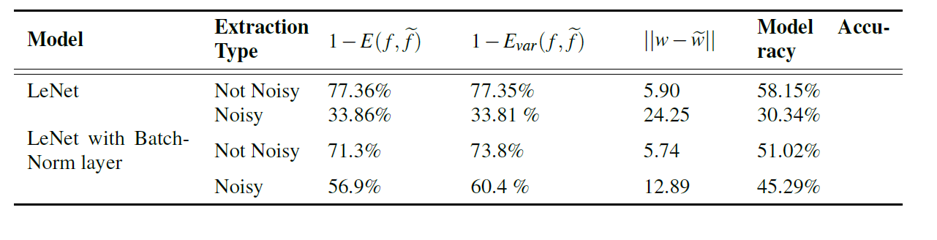
실험 결과를 해석해보면, 배치 정규화를 적용시키지 않은 모델의 경우에서, 방어 방법을 추가했을 때 그 전에 비해 추출 모델의 성능이 현저하게 떨어지는 것을 확인하여 이 방어 방법의 효율성을 증명하였습니다.
배치 정규화를 적용시켰을 때, 방어 기법을 적용하지 않았을 때에 공격자의 추출 모델의 성능은 배치 정규화를 적용시켰을 때보다 낮았지만, 방어 기법을 적용 시킨 경우를 비교하면 방어 성능이 조금 떨어진 것을 확인할 수 있었습니다. 하지만 여전히 공격자의 추출 모델이 방어 기법 적용 전 보다 떨어져, 방어 기법이 여전히 효과적이었다고 할 수 있습니다.
결론
본 연구에서는 가중치 추출 공격(Tramer’s Equation Solving attack)에 대한 방어로 Graded-Guided CAM 시각화 방법을 이용한 노이즈 추가 기법을 사용해 그 효과에 대하여 증명하였습니다.
하지만 대상이 LeNet/CIFAR-10, 마지막 층 추출로 한정되었기 때문에 다른 아키텍처·데이터셋·다층 추출·적응적 공격에 대한 일반화 검증이 추후에 추가적으로 필요할 것으로 예상됩니다.