논문명: Preventing Neural Network Weight Stealing via Network Obfuscation

저자: Kálmán Szentannai, Jalal Al-Afandi, and András Horváth

게재지: In Proceedings of the Computing Conference, 2020

URL:Preventing Neural Network Weight Stealing via Network Obfuscation

서론

보통의 Deep Neural Network는 가중치의 작은 변화가 모델 예측에 큰 변화를 주지 않습니다. 이러한 특징은 모델 추출 공격의 관점에서 이 점은 공격자에게 유리하게 작용합니다. 공격자들은 잘 학습된 원본 모델을 복제하여 가중치를 조금만 바꾸고, 그 모델이 자신의 소유라고 주장할 수 있습니다. 이러한 문제점을 해결하기 위해 본 논문에서는 원본 모델과 정확도는 동일하지만 작은 가중치 변화에도 민감한 모델을 만드는 방법을 제안합니다.

본론

Fully Connected Layer

딥러닝에서 Fully Connected Layer(FC Layer)는 입력 벡터의 모든 요소를 출력의 모든 요소와 연결하는 선현 변환 층입니다. CNN에서 Convolution Layer를 통해 모델이 이미지 내의 선, 질감, 패턴 등의 지역적인 특징을 학습하면, FC Layer는 이 특징을 바탕으로 이미지가 어떤 클래스에 속하는지 최종적으로 판단하는 역할을 합니다.

본 논문에서는 이러한 FC Layer의 구조를 변화시켜 네트워크에 혼란을 주어 가중치의 작은 변화에도 예측이 크게 바뀌는 모델을 만드는 기법을 제안합니다.

3개가 연속적으로 연결된 Fully Connected Layer를 가정하며, 각각의 층은 \(i-1, i, i+1\) 층으로 표현됩니다.

이 세 개의 연속 층에서 중간층 \(i\)를 바꿔도 끝단 매핑 \(i-1\) -> \(i+1\) 은 변하지 않도록 하는 방법으로 네트워크의 혼란을 줍니다. 중간층 \(i\)는 뉴런을 추가하는 방법으로 변화를 줍니다. 끝단 매핑은 변하지 않되, \(i-1\)와 \(i\) 사이와 \(i\)와 \(i+1\)의 매핑은 자유롭게 변화를 줄 수 있습니다.

layer \(i\)의 출력값은 다음과 같은 수식으로 표현될 수 있습니다. \(x_i = \phi\!\left( W_{i_{N\times K}}\, x_{i-1} + b_i \right)\)

  • \(N\) : \(i-1\)층의 뉴런의 개수
  • \(K\) : \(i\)층의 뉴런의 개수
  • \(W\) : 가중치
  • \(\phi\) : Relu 등의 활성화 함수
  • \(b_i\) : \(i\) 층의 bias 값

이를 토대로 \(i+1\)의 수식은 다음과 같이 표현됩니다. \(x_{i+1} = \phi\!\left( \phi\!\left( x\, W_{i-1_{N\times K}} + b_{i-1} \right)\, W_{i_{K\times L}} + b_i \right)\)

뉴런을 추가하는 방법은 크게 뉴런을 분해하는 방법과, 가짜 뉴런을 추가하는 방법이 있습니다.

뉴런 분해(Decomposing Neurons)

첫 번째 방법은, 기존의 뉴런을 0과 1사이의 \(\alpha\) 값을 이용해 두 개의 뉴런으로 분해하는 방법입니다. 이때 두 뉴런은 원래 뉴런과 동일한 bias값을 가지며, 다음 계층으로 향하는 가중치(weight)도 동일하게 물려받습니다. 이렇게하면 네트워크 전체의 입출력은 분해 전과 동일하게 유지되면서 뉴런의 개수는 증가하게 됩니다.

\[\phi\!\Big(\sum_{i=1}^{n} W^{l}_{j i}\,x_i + b^{l}_{j}\Big) \;=\; N^{l}_{j}\] \[N^{l}_{j} \;=\; \alpha\,N^{l}_{j} \;+\; (1-\alpha)\,N^{l}_{j},\qquad \alpha\in(0,1)\]

여기서 \(\alpha\,N^{l}_{j}\) 가 분해 후 첫 번째 뉴런의 출력값이 되고, \((1-\alpha)N^{l}_{j}\) 가 두 번째 뉴런의 출력값이 됩니다.

이 수식은 활성화함수가 \(\phi(x) = max(0,x)\)일 때 활성화 스위치가 같아야 하므로, 분해 전 뉴런의 bias와 분해 후 뉴런의 bias가 같아야 성립합니다.

Before decomposing neuron
After decomposing neuron

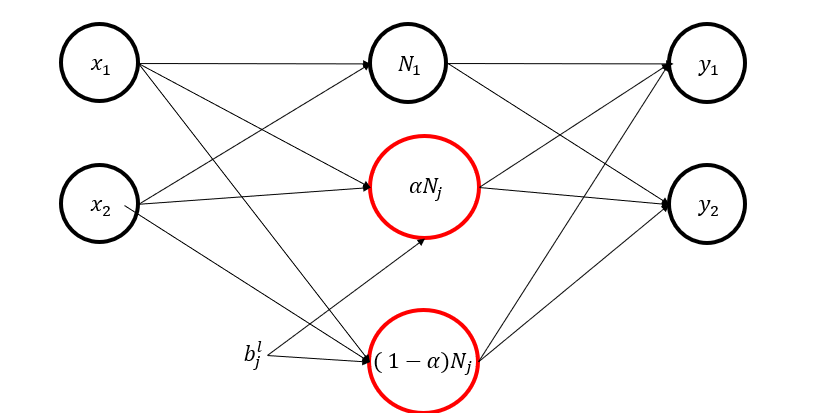
두 뉴런을 분해한 후, 새로운 뉴런들이 다음 계층과 연결될 가중치를 정해야합니다. 가장 간단한 방법은 분해 이전의 가중치를 분해 후에도 동일하게 사용하는 것입니다.

\[N^{l}_{j}\,\overline{W}^{\,l+1}_{j} \;=\; \alpha\,N^{l}_{j}\,\overline{W}^{\,l+1}_{j} \;+\; (1-\alpha)\,N^{l}_{j}\,\overline{W}^{\,l+1}_{j} \tag{7}\]

이 식은 왜 가중치를 그대로 사용해도 되는지를 보여줍니다. 좌변은 분해 전, 원래 뉴런 하나가 다음 계층에 미치는 영향입니다. 우변은 분해 후, 두 개의 새로운 뉴런이 다음 계층에 미치는 영향을 합한 것입니다 두 값이 완전히 같기 때문에, 뉴런을 두 개로 분해해도 네트워크의 최종 결과에는 아무런 변화가 없음을 수학적으로 증명합니다.

하지만 위 간단한 방법은 공격자가 네트워크 구조의 변경을 쉽게 알아챌 수 있다는 문제가 있습니다. 이 문제를 해결하기 위해, 선형대수학의 연립방정식 \(Ap = c\)을 이용하여 새로운 뉴런들이 서로 다른 가중치를 갖도록 설정합니다. 이 과정을 통해 네트워크의 내부 연결(가중치)은 완전히 바뀌지만, 전체 기능(입력에 대한 출력)은 이전과 완벽하게 동일하게 유지됩니다.

Equation System Ap = c

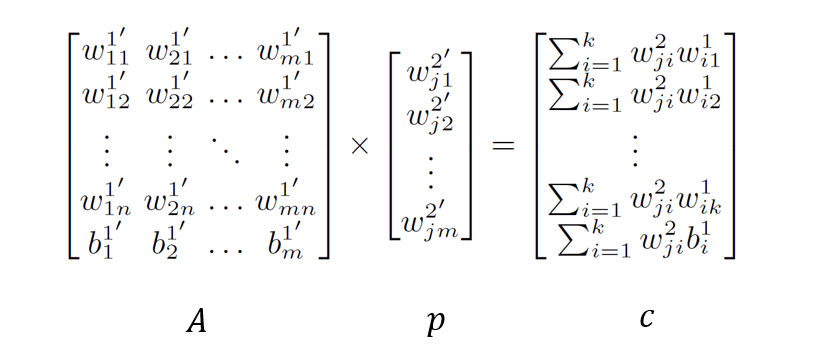
  • \(p\): 우리가 찾아야 할 미지의 값입니다. 즉, 분해된 뉴런들이 다음 계층으로 연결될 때 사용할 새로운 가중치 벡터입니다.

  • \(A\): 이미 알고 있는 값들로 구성된 행렬입니다. 분해된 뉴런들의 내부 정보(입력 가중치, bias등)를 담고 있습니다.

  • \(c\): 우리가 보존하고 싶은 목표값입니다. 원래 네트워크가 가지고 있던 연결 강도(가중치들의 곱)를 나타냅니다.

선형대수학 이론에 따르면,\(Ap = c\) 라는 방정식은 rank(\(A\)) = rank([$$A c$$]) 라는 조건을 만족할 때만 해를 가질 수 있습니다. (rank는 행렬의 계수, 즉 행렬이 표현하는 벡터 공간의 차원을 의미합니다.)

이 조건을 항상 만족시키기 위한 규칙은 \(K ≥ N + 1\) 입니다.

  • \(K\): 분해 후, 해당 계층에 있는 새로운 뉴런의 총개수
  • \(N\): 해당 계층이 받는 입력의 개수 (예: 이전 계층의 뉴런 수)
  • +1: 바이어스(bias) 항을 고려

가짜 뉴런(Deceptive Neurons)

단순히 뉴런을 분해하는 것만으로는 공격자가 바이어스(bias) 값 등을 분석하여 조작을 탐지할 수 있으므로, 이를 숨기기 위해 가짜 뉴런을 추가하는 전략을 사용합니다. 이 가짜 뉴런들은 서로의 효과를 상쇄시켜 총합이 0이 되도록 하여 네트워크의 기능에는 영향을 미치지 않도록 설계됩니다. 진짜 뉴런과 가짜 뉴런을 섞어 그룹으로 만들면 공격자가 어느 것이 진짜이고 가짜인지 구별하는 것은 기하급수적으로 어려워져 사실상 분석이 불가능해집니다.

가짜 뉴런들은 항상 한 쌍으로 생성되어 서로의 효과를 서로 상쇄시킵니다. 동일한 bias를 가지는 그룹 내에 진짜 뉴런과 가짜 뉴런 쌍을 만들어 공격자가 보기에 이 그룹 내의 뉴런들의 특성이 비슷해 어느 것이 진짜이고 가짜인지 구별하기 힘들게 만듭니다.

Experiment

간단한 수치 설정으로 먼저 뉴런 분해 방법의 성능을 검증하였습니다.

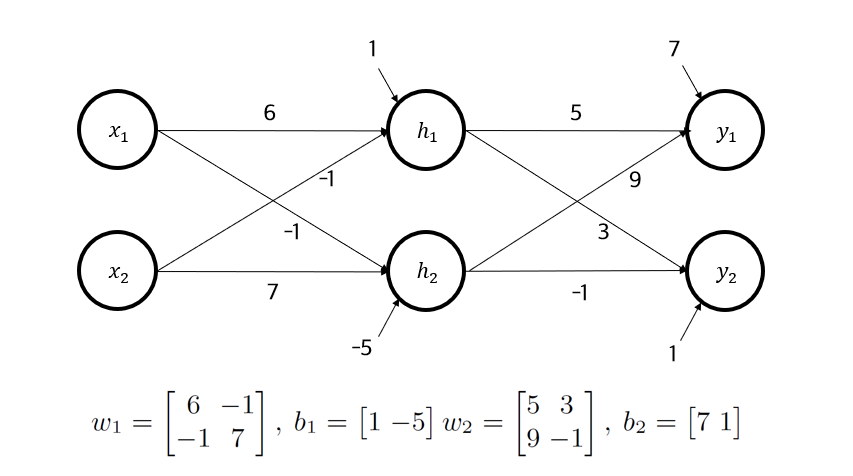
Simple Experiment for Decomposing Neurons-1

위 구조에서 중간 계층 뉴런들을 분해해 4개 뉴런으로 만들고, 연립방정식을 활용해 가중치를 찾아냈습니다.

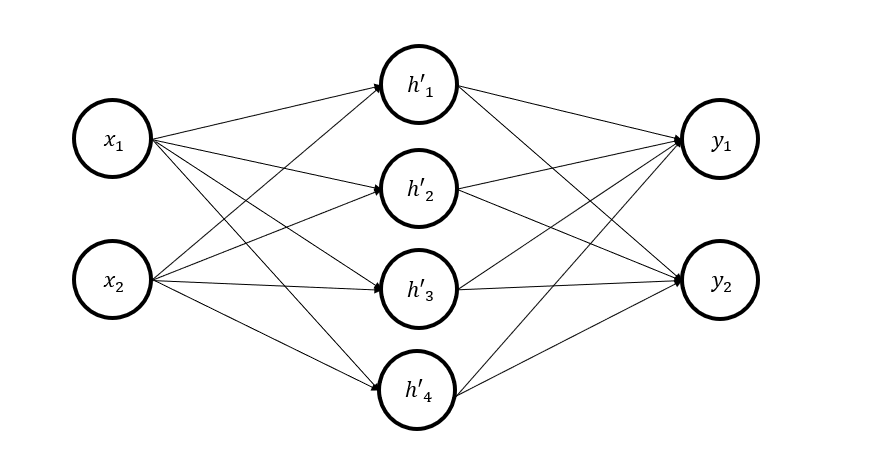
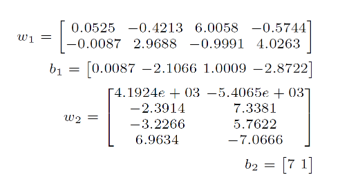
Simple Experiment for Decomposing Neurons-2
Simple Experiment for Decomposing Neurons-3

이후 입력 벡터를 [7,9]로 설정한 뒤, 가중치에 1%의 노이즈를 랜덤으로 주입하여 출력값의 변화를 관찰하였습니다.

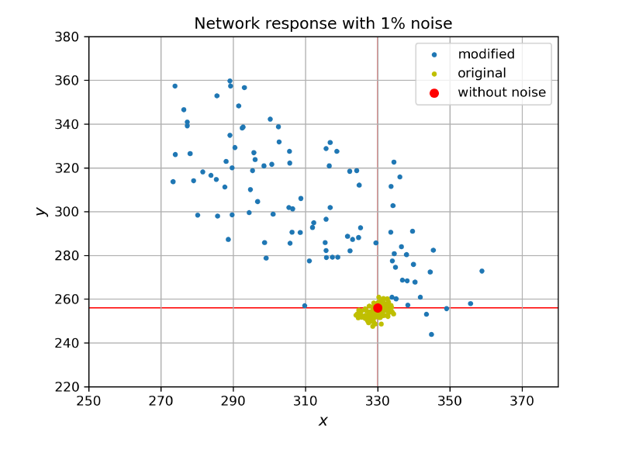
Simple Experiment for Decomposing Neurons-4

그래프를 보면 뉴런을 분해한 모델에 노이즈를 추가하였을 때 출력값의 분포가 원본 모델에 노이즈를 추가하였을 때 출력값의 분포보다 훨씬 더 넓게 퍼져있는 것을 볼 수 있습니다. 이를 통해 뉴런을 분해하는 방법으로 가중치의 변화에 출력값이 민감하게 반응하도록 한 기법이 효과적으로 적용되었음을 알 수 있습니다.

이후, 더 복잡한 구조로 추가 실험을 진행하였습니다. 실험 환경은 다음과 같습니다.

  • 네트워크 아키텍쳐 : 5층의 fc layer(input layer, 3 hidden-layers, output layer)
  • 뉴런 개수 : 각각 728개, 32개, 32개, 32개, 10개
  • 데이터셋 : MNIST[8]
  • 배치 크기 : 32
  • 최적화함수 : Adam
  • 반복 수 : 7500
  • 모델 훈련 후 테스트셋 정확도 : 98.4%

모델을 학습한 뒤, 앞서 설명드린 방법으로 모델에 추가 뉴런을 9,18,36,72개로 다르게 생성하여 실험하였습니다. 추가 뉴런은 각 3개의 은닉 층에 동일한 개수로 생성되며, 2/3는 가짜 뉴런 쌍, 1/3는 뉴런 분해로 생성되었습니다. 예를 들어, 36개를 추가로 생성한 경우 4x2개가 가짜 뉴런 쌍, 4개가 분해 뉴런으로 각 층에 추가됩니다.

이렇게 모델을 새롭게 만든 뒤, 각각의 경우에 가중치에 노이즈를 추가해가며 모델의 테스트셋에 대한 정확도를 측정하였습니다.

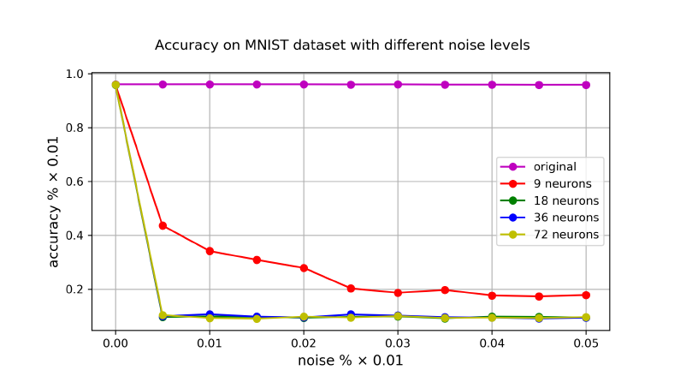
Accuracy on MNIST dataset with different Noise Levels

그래프를 확인해보면 노이즈를 추가하지 않았을 경우 작은 노이즈에 강건한 모델의 모습을 볼 수 있습니다. 하지만 추가된 모델들은 일정 수준 이상의 작은 노이즈가 주입되었을 때 정확도가 급격하게 낮아지는 모습을 확인할 수 있습니다.

이후 모델들을 다양한 최적화함수(SGD, AdaGrad, Adam)들과 다양한 스텝 사이즈를 적용시키며 추가적으로 학습한 후에 가중치 변화에 얼마나 정확도가 민감하게 반응하는지 추가 실험을 진행하였습니다. 결과는 다음과 같습니다.

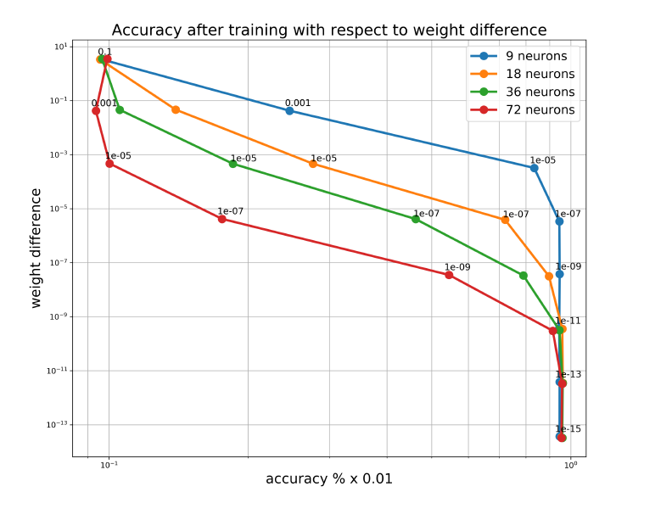
Accuracy on MNIST dataset with Additional Training

역시 은닉 수준을 높일수록(뉴런을 더 많이 추가할수록) 작은 노이즈에도 모델의 정확도가 크게 감소하는 결과를 확인할 수 있었습니다.

이후 공격 방법중 하나인 지식 증류(Knowledge Distillation)을 적용했을 때 이 방어 기법의 효과에 대하여 실험하였습니다. 지식 증류는 1백만 개의 무작위 입력 샘플로 학생 모델을 학습시키는 방법으로 이루어졌습니다.

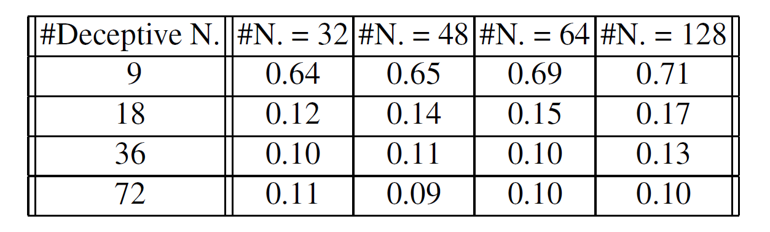
Accuracy on MNIST dataset with Knowledge Distillation

그래프의 열은 공격자가 사용한 은닉 층의 뉴런 개수이며, 행은 원본 모델에 추가된 뉴런의 개수입니다. 결과를 보면 은닉 뉴런이 18개 이상일 때 학생 모델의 정확도가 10% ~ 17% 수준으로 급락합니다. 이는 MNIST 데이터셋(클래스 10개)에서 무작위로 추측하는 것과 비슷한 수준으로, 사실상 기능 복제에 완전히 실패했음을 의미합니다. 이 실험을 통해 지식 증류와 같은 정교한 모델 복제 공격에 대해서도 제안된 방어 기법이 매우 강력한 방어 능력을 가지고 있음을 증명하였습니다.

결론

본 논문에서는 모델의 원래 성능과 기능은 유지하면서 내부 가중치의 변화에 민감한 모델을 추가 뉴런을 만드는 방식으로 만들어 가중치의 작은 변화를 준 복제 모델을 만드는 모델 추출 공격에 대한 방어 기법을 제시하고 그 성능을 성공적으로 증명하였습니다. 이는 네트워크 모델의 지적 재산권을 보호하고 무단 도용 및 수정을 효과적으로 방지하는 효과를 가져올 수 있습니다.