논문명: Perturbing Inputs to Prevent Model Stealing

저자: Justin Grana

게재지: IEEE Conf. on Communications and Network Security, Avignon, France, 2020.

URL: Perturbing Inputs to Prevent Model Stealing

서론

클라우드 기반 머신러닝 서비스는 주로 입력 \(x\)에 대한 예측 \(f(x)\)를 반환하는 API 형태로 제공됩니다. 공격자들은 해당 서비스에 반복적으로 질의하여 얻은 결과를 바탕으로 모델의 파라미터를 추정하거나 모델의 복제를 시도합니다. 이러한 공격에 대한 기존의 방어는 출력의 반올림(rounding), 노이즈 삽입, 질의 요청 모니터링, 워터마킹(watermarking) 등 출력의 사후 조작이나 사후 검출에 치우쳐 있으며, 질의가 충분히 많아질 때에는 효과가 떨어질 수 있는 한계가 있습니다.

본 논문은 출력이 아닌 입력을 가공(garbling)하여 내생성(endogeneity)을 인위적으로 생성해 공격자의 추정이 무한표본에서도 실제 값에 수렴하지 않도록 하는 방법을 제안합니다.

기존 방식(상단)과 제안 방식(하단)

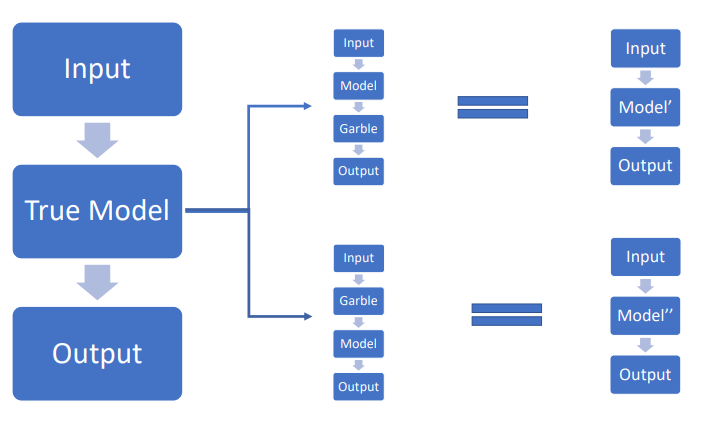
사전지식

추정 함수 \(h\)

공격자는 추정 함수 h를 통해 수집한 데이터 \((X,\hat{Y})\)를 바탕으로 파라미터 \(\Theta\)를 추정합니다: \(\begin{align} h:X^N \times Y^N \to \Theta \end{align}\)

공격자 추정기: OLS, MLE

공격자는 다음 두가지의 방식을 통해 파라미터를 추정하고자 합니다.

  • OLS(최소제곱법)는 잔차 제곱합 \(\sum(\hat y_i-\alpha-\beta x_i)^2\)를 최소화해 파라미터 \((\hat\alpha,\hat\beta)\)를 구하는 방법입니다.
  • MLE(최대우도법)는 데이터가 주어졌을때 우도(likelihood)또는 로그우도를 최대화하는 파라미터를 구하는 방법입니다. 가우시안 선형에서는 OLS와 동일해지며, 로지스틱에서는 \(\sum_i{y_i \log{p_i} + (1-y_i)\log{(1-p_i)}}\)를 최대화합니다.

핵심은 입력 가공으로 변수와 오차의 상관이 생겨 OLS/MLE 모두 대표본에서 한계 편향을 갖게 된다는 점입니다.

평가 지표

방어의 성능을 평가하기 위해 다음 두가지 지표를 사용합니다.

  • 공격자의 한계 추정 오차는 다음과 같습니다: \(\begin{align} D=\mathrm{plim}\,h(X,\hat Y)-\theta \end{align}\)
  • 서비스의 예측 오차는 다음과 같습니다: \(\begin{align} \sigma^2=\mathbb{E}[(f_\theta(x)-f_\theta(g(x)))^2] \end{align}\) 목표는 \(D\)는 크게, \(\sigma^2\)는 작게 유지하는 것입니다.

제약 사항

본 논문에서는 다음과 같은 제약을 적용합니다: \(\begin{align} \frac{1}{|X|}\sum\mathbb{E}[x-g(x)]=0 \end{align}\) 이는 평균적으로 입력의 이동이 없음을 보이기 위한 제약입니다. 실제로는 이 제약이 없어도 제안 방법은 잘 작동하며, 핵심 결과(편향·분산 구조)는 유지됩니다.

본론

단순 선형회귀: 대표본 결과(Prop. 1)

  • 대표본 (Large Sample) 가장 단순한 경우로, 하나의 변수를 갖는 선형 머신 러닝 모델을 다음과 같이 정의합니다: \(\begin{align} f_{\theta}=\alpha+\beta x \end{align}\) 입력을 가공하기 위한 함수는 다음과 같습니다: \(\begin{align} g(x)=x+\gamma(\mu(x,\lambda^2)) \end{align}\) 이때, \(\mu(a,b)\)는 정규분포 \(\mathcal{N} (a,b)\)를 따르는 변수입니다.

    위를 바탕으로 가공이 적용된 예측 결과 \(\hat{y}\)는 다음과 같이 표현됩니다: \(\begin{align} \hat y=\alpha+\beta g(x) \end{align}\)

    \[\begin{align} =\alpha+(1+\gamma)\beta x+\beta\gamma\lambda\varepsilon \quad \varepsilon \sim \mathcal{N}(0,1) \end{align}\]

    따라서 공격자의 추정 오차 \(D\)는 다음과 같습니다: \(\begin{align} \mathrm{plim}\,\hat\beta=(1+\gamma)\beta \quad\Rightarrow\quad \,D=\beta\gamma \end{align}\) 서비스의 예측오차 \(\sigma^2\)는 다음과 같습니다: \(\begin{align} \sigma^2=(\beta\gamma)^2\{\mathrm{Var}(x)+\lambda^2\} \end{align}\) 즉 대표본에서 \(D\)는 \(\gamma\)에만 비례하고, \(\sigma^2\)는 \(\gamma\)와 \(\lambda\)에 의해 커집니다.

  • 유한표본(Small Sample)

    공격자가 유한한 질의 갯수로 OLS 또는 MLE를 통해 \(\beta\)를 추정하고자 하면 다음이 성립합니다: \(\begin{align} \mathbb{E}[(\beta-\hat\beta)^2]=(\beta\gamma)^2+(\beta\gamma\lambda)^2\, \mathbb{E}\!\Big[\big(\sum_{i=1}^n x_i^2\big)^{-1}\Big] \end{align}\) 즉, \(\lambda\)가 커질수록 유한표본에서 공격자가 추정한 파라미터 \(\hat{\beta}\)와 실제 파라미터 \(\beta\)의 오차가 커지게 됩니다.

    따라서 유한표본에서 0보다 큰 \(\lambda\)는 공격자의 파라미터 추출을 더욱 어렵게 합니다.

  • 식별 위험

    공격자는 OLS 또는 MLE를 통해 모델의 파라미터 \(\hat{\alpha}\)와 \(\hat{\beta}\), 모델의 분산 \(\hat{\Sigma}^2 = \sum^N_{i=1}(\hat{y}-(\hat{\alpha}+\hat{\beta}x_i))^2\)을 추정할 수 있습니다. 이때, 공격자가 \(\lambda\)를 알고 있다면 다음과 같이 실제 파라미터를 복원할 수 있습니다: \(\begin{align} \hat{\Sigma}^2 \rightarrow (\beta\gamma\lambda)^2 \qquad(\hat{\Sigma}\to|\beta\gamma\lambda|) \end{align}\) \(\begin{align} \beta\gamma=\frac{\hat{\Sigma}}{\lambda},\qquad \hat\beta=\beta+\beta\gamma \ \Rightarrow\ \,\beta=\hat\beta-\frac{\hat{\Sigma}}{\lambda} \end{align}\) 그러므로 \(\gamma,\lambda\)는 비공개로 유지하고 랜덤화가 적용되어야 합니다.

로지스틱 회귀

로지스틱 회귀 모델은 다음과 같습니다:

\[\begin{align} \hat y=\sigma\!\big(\alpha+\beta\,g(x)\big),\qquad \sigma(z)=\frac{1}{1+e^{-z}} \end{align}\]

로짓(선형 점수) 공간에서는 선형과 동일하게 다음이 성립합니다:

\[\begin{align} \mathrm{plim}\,\hat\beta=(1+\gamma)\beta \quad\Rightarrow\quad \,D=\beta\gamma \end{align}\]

한편 확률 공간에서는 시그모이드 함수의 기울기가 꼬리에서 작기 때문에, \(\gamma\)가 커져도 확률 오차의 증가는 완만하게 나타납니다.

다음은 로지스틱 회귀 모델에서 \(\gamma\)에 따른 \(D\), \(\sigma^2\), 로짓 오차의 시각화 결과입니다:

gamma 증가에 따른 로짓 오차와 공격자 추정 오차, 서비스 예측 오차

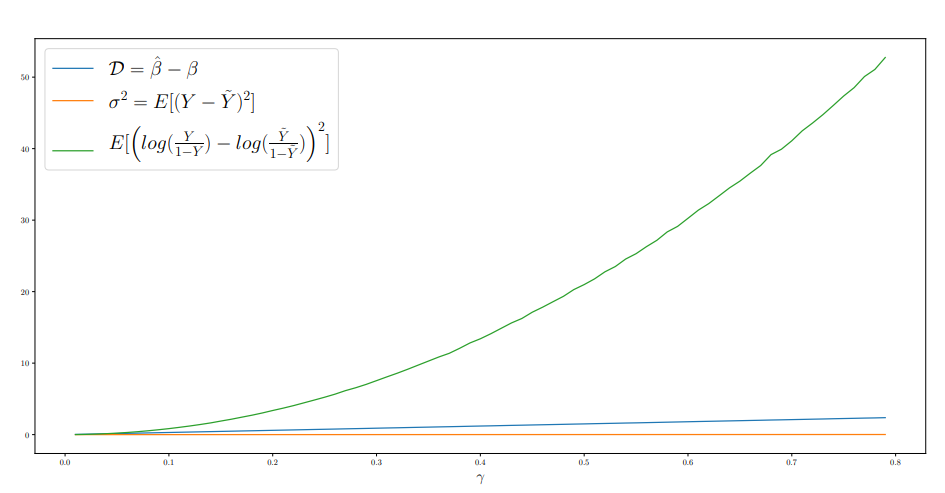
\(\gamma\)가 증가할 때 로짓 오차는 지수적으로, 추정 오차(\(D\))는 선형적으로 증가하는 반면, 서비스의 예측인 확률의 오차(\(\sigma^2\))는 완만하게 증가합니다.

다변량·다중 가공(Prop. 4)

다음과 같은 ML 서비스를 가정합니다: \(\begin{align} \hat{y} = f_{\theta} = \alpha + \beta_1 x_1 + \beta_2 x_2 \end{align}\) 각 \(x_i\)에 대해 다음의 가공을 적용합니다. \(\begin{align} g(x_i)=x_i+\gamma_i\,\mu_i(x_i,\lambda) \end{align}\)

공격자가 파라미터들에 대해 OLS 또는 MLE로 추정을 시도한다고 가정합니다. 이때 다음과 같은 수식들이 성립합니다: \(\begin{align} \mathrm{plim}(\hat{\beta}_i)-\beta_i = \beta_i \gamma_i \end{align}\) \(\begin{align} \sigma^2 = [(\beta_1 \gamma_1)^2Var(x_1) + (\beta_2 \gamma_2)^2Var(x_2)+2\beta_1\beta_2\gamma_1\gamma_2\,\mathrm{Cov}(x_1,x_2)+(\lambda(\gamma_1 \beta_1 + \gamma_2 \beta_2))^2] \end{align}\) 즉 편향의 규모는 단일 교란의 경우와 동일하게 \(\gamma_i\)가, 서비스 예측 오차는 입력 공분산 \(\Sigma\)와 \(\lambda\)가 좌우함을 보여줍니다.

결론

본 논문은 입력 가공(garbling) 으로 내생성(endogeneity) 을 유발하여, 공격자가 무한표본에서도 모델의 파라미터 추정에 실패하도록 만드는 방어를 제시합니다. 방어의 성과는 공격자 측 추정 오차 \(D\)와 서비스 측 예측 오차 \(\sigma^2\)의 균형으로 평가되며, 핵심 메시지는 다음과 같습니다.

  • 비일관화의 축: \(\gamma\)는 추정한 파라미터의 한계 편향을 만들며 이는 표본 수와 무관합니다. \(\lambda\)는 유한표본 분산을 키워 초기·제한 질의에서 복제를 어렵게 합니다.
  • 서비스 손실 관리: \(\sigma^2\)는 모델·데이터 분포와 \(\gamma,\lambda\)로 결정되며, 선형에서는 \(\sigma^2\)가 입력 공분산과 \(\lambda^2\) 항으로 분해됩니다. 로지스틱에서는 시그모이드 꼬리의 저민감도를 이용해, 로짓 공간 왜곡은 크게 하면서도 확률 공간의 손실을 작게 유지할 수 있습니다.
  • 다변량 확장: 좌표별 가공으로 각 계수의 편향이 \(\beta_i\gamma_i\)만큼 발생합니다. 입력 공분산 \(\Sigma\)는 외부 입력에 의존하지만, 방어자는 \(\gamma\)의 부호·크기를 설계하여 같은 편향 크기에서 \(\sigma^2\)를 더 작게 만들 수 있습니다.
  • 식별 위험: 공격자가 \(\lambda\)를 알면 잔차 표준편차 \(\hat\Sigma\)와 \(\hat\beta\)로 실제 파라미터를 복원할 수 있으므로 \(\gamma,\lambda\)의 비공개·랜덤화가 필수입니다.

범위·한계

분석은 선형·로지스틱 모형에 초점을 맞춘 개념 증명 수준입니다. 대규모 비선형(DNN 등) 모델에 대한 이론과 실증, 적응형 공격을 실행하는 공격자와의 동적 상호작용(게임이론적 균형), 운영 환경에서의 튜닝·모니터링 절차는 후속 과제로 남습니다. 또한 입력 분포(및 공분산)는 외부 입력에 의존하므로, 방어자는 이를 바꾸기보다 관찰된 분포에 맞춘 가공 설계로 손실을 관리한다는 점이 전제입니다.