논문명: Data-Free Model Extraction

저자: Jean-Baptiste Truong, Robert J. Walls, Pratyush Maini, Nicolas Papernot

게재지: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2021

URL: Data-free model extraction

서론

기존의 모델 추출 공격(Model Extraction Attack)은 피해자 모델(Victim Model)의 학습 데이터와 유사한 대리 데이터셋(Surrogate Dataset)에 접근할 수 있다는 가정을 전제로 하고 있습니다. 하지만 실제로 완전한 블랙박스 모델을 타겟으로 하는 공격에서는 모델의 학습 단계에서 어떠한 데이터셋이 사용되었는지 알기 어렵습니다.

본 연구에서는 대리 데이터셋이 필요하지 않은 데이터 프리 모델 추출 공격(Data-Free Model Extraicton)을 제안합니다. 즉, 별도의 학습용 데이터 없이도 피해자 모델을 추출할 수 있도록 하는 새로운 방식을 제시합니다.

사전지식

지식 증류(Knowledge Distillation)

지식 증류(Knowledge Distillation)이란, 이미 학습된 대규모 모델(Teacher)의 예측 정보를 활용하여 작은 규모의 모델(Student)이 이를 모방하도록 학습시키는 지식 전이 기법입니다.

주로 Teacher–Student 구조를 사용하며, Student 모델은 입력 데이터를 Teacher 모델에 질의(query)하여 얻은 출력 분포(soft label)나 로짓(logit)을 학습 목표로 삼습니다.

지식 증류는 대규모 모델의 정확도는 유지하면서 모델의 규모를 줄이기 위해 사용됩니다.

지식 증류 수행 시, 일반적으로 모델의 소유자가 수행하기 때문에 Teacher 모델의 학습 데이터셋을 알고 있는 경우가 많습니다. 하지만 데이터셋의 규모가 너무 크거나, 보안상의 이유로 데이터셋에 대한 접근이 불가능한 경우가 종종 있습니다. 이럴 때 사용하는 접근법이 데이터 프리 지식 증류(Data-Free Knowledge Distillation, DFKD)입니다.

데이터 프리 지식 증류(Data-Free Knowledge Distillation, DFKD)

원본 데이터에 대한 접근 권한이 없는 상황에서, 지식 증류를 하기 위해서는 Student 모델이 Teacher 모델에 질의할 입력 데이터를 새로 만들어내야 합니다.

DKFD 기법에서는 그 역할을 입력 데이터 생성기(Generator)가 수행합니다.

Teacher 모델의 출력값을 활용해 Generator를 학습시키고, 이렇게 학습된 Generator는 Student가 Teacher에 질의하기에 최적화된 입력 데이터를 생성합니다.

이를 통해 원본 데이터 없이도 Teacher의 지식을 Student 모델로 효과적으로 전이할 수 있습니다.

본문에서 제시하는 데이터 프리 모델 추출 공격(Data-Free Model Extraction)은 위에서 설명드린 DFKD의 작동 방식에서 영감을 얻어 이를 모델 추출 공격에 활용하였습니다.

본론

데이터 프리 모델 추출 공격(Data-Free Model Extracton)

Data-Free Model Extraction에서는 지식 증류의 기법을 활용하여, 타겟 모델(Victim)을 Teacher 모델로 설정하고, 공격자의 추출 모델을 Student 모델로 설정합니다. 그리고 Student 모델이 Victim 모델을 잘 모방할 수 있도록 Generator가 최적의 쿼리를 생성합니다.

Generator는 최적의 쿼리를 생성하도록 파라미터가 학습되고, Student 모델은 그 쿼리에 대해 Victim 모델과 가장 유사한 출력값을 내도록 파라미터가 학습됩니다.

여기서 최적의 쿼리란, Victim 모델의 결정 경계(Dicision surface)와 Student 모델의 결정 경계 간의 불일치를 가장 잘 드러내는 쿼리입니다. 쉽게 말해, Student 모델이 Victim 모델과 일치하는 출력을 내는 것이 가장 어려운 입력 데이터 쿼리를 의미합니다.

따라서 Generator는 Victim 모델과 Student 모델의 손실을 최대화하는 방향으로 학습이 이루어집니다.

반면 Student 모델의 목표는 Victim 모델과 가장 유사한 모델을 만드는 것이 목표이기 때문에, 손실을 최소화하는 방향으로 학습이 이루어집니다.

이러한 Generator와 Student 모델의 관계는 적대적 신경망 모델(Generative Adversarial Networks)의 Generator와 분류기(Discriminator)의 관계와 유사합니다.

Data-Free Model Extraction의 최종 목표를 수식으로 표현하면 다음과 같습니다.

\[\arg\min_{\theta_S} \; \mathbb{P}_{x \sim \mathcal{D}_V} \left( \arg\max_i \mathcal{V}_i(x) \neq \arg\max_i \mathcal{S}_i(x) \right)\]
  • \(\mathcal{D}_V\): Victim 모델의 학습에 사용된 입력 데이터 도메인
  • \(\theta_S\): Student 모델의 파라미터 집합
  • \(\mathbb{P}_{x \sim \mathcal{D}_V}\): 데이터 풀 \(\mathcal{D}_V\)에서 \(x\)를 샘플링하는 과정
  • \(\mathcal{V}_i(x)\): Victim 모델이 \(x\)에 대해 클래스 \(i\)일 확률(또는 logit)
  • \(\mathcal{S}_i(x)\): Student 모델이 \(x\)에 대해 클래스 \(i\)일 확률(또는 logit)
  • \(\arg\max_i\): 가장 높은 값을 갖는 클래스 인덱스 반환

수식은 Victim 모델의 학습에 사용된 입력 데이터 도메인에서 샘플링한 데이터에 대해 Student 모델의 파라미터를 최적화하여, Student 모델과 Victim 모델의 예측 불일치를 최소화하는 것을 목표로 한다는 의미입니다.

하지만 Data-Free 모델이기 때문에, \(\mathcal{D}_V\)에 대한 접근이 불가능하다는 것을 가정합니다. 따라서 Generator에서 만든 합성 입력 데이터를 사용합니다. 이것을 바탕으로 재구성한 모델의 목표를 수식으로 표현하면 다음과 같습니다.

\[\arg\min_{\theta_S} \; \mathbb{E}_{x \sim \mathcal{D}_S} \left[ \mathcal{L}(\mathcal{V}(x), \mathcal{S}(x)) \right]\]
  • \(\mathcal{D}_S\): 생성된(Synthesized) 데이터셋
  • \(\mathbb{E}_{x \sim \mathcal{D}_S}\): 데이터셋 \(\mathcal{D}_S\)로부터 \(x\)를 샘플링하여 계산한 손실 \(\mathcal{L}\)의 평균
  • \(\mathcal{L}(\mathcal{V}(x), \mathcal{S}(x))\): Victim 모델 \(\mathcal{V}\)와 Student 모델 \(\mathcal{S}\)의 출력 간 손실 함수

이러한 목표를 가진 Data-Free Model Extraction의 작동 방식은 그림과 같습니다.

   
       
   
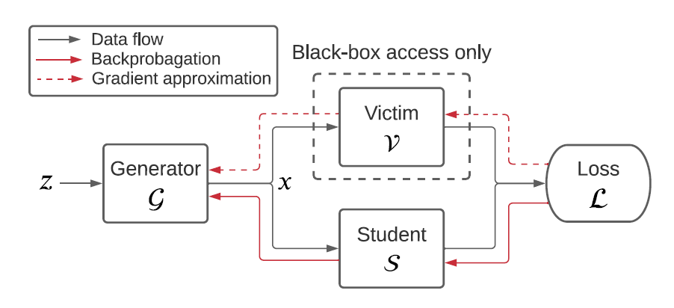
    Diagram of the Data-Free Model Extraction

정규분포를 따르는 무작위의 노이즈 \(z \sim \mathcal{N}(0, 1)\)이 Generator에 입력값으로 들어가면, Generator는 합성 데이터 쿼리를 Student 모델과 Victim 모델에게 보냅니다.

이후 Student 모델은 Victim 모델의 출력값과의 차이에 대한 손실을 계산하여 손실을 최소화하는 방향으로 역전파(backpropagation)를 통해 파라미터를 학습합니다.

Generator은 그 손실을 최대화하는 방향으로 학습이 이루어집니다.

모델의 목표를 수식으로 나타내면 다음과 같습니다.

\[\min_{S} \max_{G} \; \mathbb{E}_{z \sim \mathcal{N}(0, 1)} \left[ \mathcal{L}(\mathcal{V}(\mathcal{G}(z)), \mathcal{S}(\mathcal{G}(z))) \right]\]

여기서 Student 모델과 Generator의 역전파 과정에서 차이점은, 역전파를 위해 Student 모델은 자신의 출력값과 Victim 모델의 출력값만을 필요로 하지만 Generator는 Victim 모델의 기울기(gradient)또한 필요로 한다는 점입니다. Student 모델과 Victim 모델이 가장 구분하기 힘들어하는 쿼리를 만들도록 파라미터를 학습하기 때문입니다.

하지만 블랙 박스 모델인 Victim 모델의 기울기는 공개되지 않습니다. 그렇기 때문에 공개되지 않은 Victim 모델의 기울기를 찾아내는 기울기 근사(gradient approximation) 기법을 필요로 합니다.

블랙박스 기울기 근사(Black-box Gradient Approximation)

Black-box Gradient Approximation은 블랙박스 모델의 내부 파라미터나 실제 gradient에 접근할 수 없는 상황에서 gradient를 추정하는 기법입니다.

특히 Zeroth Order Optimization 방법을 사용하면, 모델의 출력값만을 기반으로 기울기를 근사할 수 있습니다.

이 과정에서는 입력 \(x\)에 아주 작은 변화(perturbation) \(\epsilon\)을 주고, 모델 출력의 변화를 관찰하여 gradient를 추정합니다. 수식으로 표현하면 다음과 같습니다.

\[\nabla f(x) \approx \frac{f(x + \epsilon) - f(x)}{\epsilon}\]

여기서 \(f(x)\)는 모델의 출력 함수이며, \(\epsilon\)은 매우 작은 값입니다.

이 방법의 핵심은 블랙박스 환경에서 직접 gradient를 얻을 수 없을 때 입력을 미세하게 변형시키고 그에 따른 출력 변화를 비교함으로써 gradient를 간접적으로 계산하는 것입니다. Victim 모델의 기울기는 이러한 방식으로 근사됩니다.

이 때, 여러개의 서로 다른 \(\epsilon\)값을 사용하면 더 정확한 기울기를 근사할 수 있게 됩니다. 따라서 정확도는 높아지지만, 그만큼 많은 질의를 필요로 하게되므로 질의의 복잡도(Complextity of Quries)가 커지게 됩니다. 반대의 경우, 정확도는 낮아지지만 질의의 복잡도도 낮아지게 됩니다.

따라서 적절한 서로 다른\(\epsilon\)값의 개수를 찾아내는 것이 중요합니다.

손실 함수(Loss Function)

Student 모델과 Vicitm 모델의 차이를 계산하기 위해 손실 함수를 설정해야합니다.

전통적으로는 Kullback–Leibler (KL) Divergence가 널리 사용됩니다. 이는 지식 증류에서에서 Student 모델의 출력 분포를 Victim 모델과 정렬시키는 데 효과적입니다. KL Divergence의 수식은 다음과 같습니다.

\[\mathcal{L}_{\mathrm{KL}}(x) = \sum_{i=1}^K \mathcal{V}_i(x) \log \left( \frac{\mathcal{V}_i(x)}{\mathcal{S}_i(x)} \right)\]

여기서 \(\mathcal{V}_i(x)\)와 \(\mathcal{S}_i(x)\)는 각각 Victim과 Student 모델이 클래스 \(i\)에 대해 예측한 확률입니다.그러나 KL Divergence는 기울기 소실(vanishing gradient) 문제를 겪을 수 있다는 한계가 있습니다.

이 한계를 극복하기 위해 L1 norm loss가 사용되기도 합니다. L1 loss는 Victim과 Student 모델의 logit 값 차이를 직접 계산하며, 기울기 소실 문제를 피할 수 있습니다. 이 때, Victim의 logit 값은 softmax 출력값으로부터 추정할 수 있다고 가정합니다.

수식은 다음과 같습니다.

\[\mathcal{L}_{\ell_1}(x) = \sum_{i=1}^K \left| v_i - s_i \right|\]

실제로 입력 \(x\)에 대한 KL Loss의 기울기 크기는, Student가 Victim에 가까워질수록 L1 Loss의 기울기보다 훨씬 작아지는 경향이 있습니다. 따라서 L1 Loss는 특히 두 모델이 이미 유사한 예측을 하는 상황에서 학습을 더 안정적으로 유지할 수 있습니다.

실험(Experiment)

알고리즘(Algorithm)

실험을 위한 알고리즘은 다음 그림과 같습니다.

Algorithm of the Data-Free Model Extraction

이 구조에서 Generator \(G\)와 Student \(S\)는 번갈아 가며 학습을 진행합니다. 하나의 반복(iteration)에서 먼저 Generator를 일정 횟수 \(n_G\) 학습한 후, Student를 일정 횟수 \(n_S\) 학습하는 방식입니다.

  1. Generator 학습 단계 (\(n_G\)회 반복)

    • \(z \sim \mathcal{N}(0, 1)\) 샘플링

    • \(x = G(z; \theta_G)\) 생성

    • 손실 계산

    • Gradient Approximation을 사용하여 \(\nabla_{\theta_G} \mathcal{L}(x)\)를 근사

    • Generator는 손실을 최대화하도록 업데이트

      \[\theta_G \leftarrow \theta_G + \eta \, \nabla_{\theta_G} \mathcal{L}(x)\]

  2. Student 학습 단계 (\(n_S\)회 반복)

    • \(z \sim \mathcal{N}(0, 1)\) 샘플링

    • \(x = G(z; \theta_G)\) 생성

    • 손실 계산

    • Student는 손실을 최소화하도록 업데이트

    \[\theta_S \leftarrow \theta_S - \eta \, \nabla_{\theta_S} \mathcal{L}(x)\]

이 때 \(n_G\)와 \(n_S\)의 비율에 따라 학습 특성이 달라집니다.

  • \(n_G\)는 높고, \(n_S\)는 낮은 경우

    Generator가 더 많은 학습을 하므로 어려운 예제를 많이 생성하지만 Student가 이를 충분히 학습하지 못할 수 있습니다.

  • \(n_G\)는 낮고, \(n_S\)는 높은 경우

    Student는 많이 학습하지만, 어려운 예제에 대한 학습이 부족할 수 있습니다.

Generator에서의 기울기 근사(Gradient Approximation)

본 연구에서 기울기 근사(Gradient Approximation)는 Foward Diffrent Method 방법으로 수행되며, 다음과 같은 수식으로 표현됩니다.

\[\nabla_{\text{FWD}} f(x) = \frac{1}{m} \sum_{i=1}^m d \frac{f(x + \epsilon \mathbf{u}_i) - f(x)}{\epsilon} \mathbf{u}_i\]
  • \(\mathbf{u}_i\) : 무작위 방향 벡터
  • \(m\) : 방향 벡터 \(\mathbf{u}_i\)의 개수
  • \(\epsilon\) : 추가된 작은 변화(perturbation)
  • \(f\) : 손실 함수

전에서 언급했듯이 무작위 방향 벡터의 개수를 의미하는 \(m\)값에 따라서 질의의 개수가 달라지고, 이 값이 높아질수록 정확도와 질의 개수가 상승합니다.

실험 환경 설정

실험을 위한 환경 설정은 다음과 같습니다.

모델(Model) 아키텍처 (Architecture) 최적화 함수(Optimizer) 학습률(Learning Rate) 학습 주기(Epoch) 비고
Victim (ResNet-34–8x) SGD 0.1 50 (SVHN) / 200 (CIFAR-10) 쿼리 예산 : 2백만 개 (SVHN), 2천만 개M (CIFAR-10)
Student ResNet-16–8x SGD 0.1 50 (SVHN) / 200 (CIFAR-10) -
Generator 3 Conv + BatchNorm + ReLU Adam 5×10⁻⁴ 50 (SVHN) / 200 (CIFAR-10) 기울기 근사 : m=1, ε=10⁻³

Victim 모델은 ResNet-34-8x을 사용하였고, 위와 같은 세팅으로 SVHN 데이터셋과 CIFAR-10 데이터셋을 학습시켰습니다.

이후 위에 언급한 알고리즘에 따라 Student 모델과 Generator를 학습시켰습니다.

실험 결과

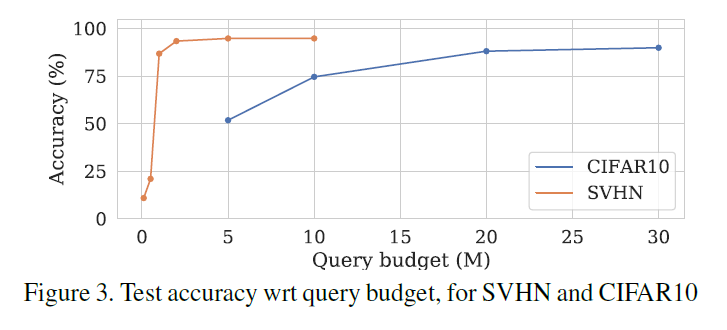
Test accuracy wrt query budget, for SVHN and CIFAR10

위 그래프는 쿼리 예산이 높아질수록 Student 모델이 어떻게 변하는지 실험한 결과를 나타냅니다.

비교적 간단한 데이터셋인 SVHN의 경우 약 2백만개 쿼리 예산을 사용하였을 때부터 최적의 정확도로 수렴하였고, 조금 더 복잡한 CIFAR-10 데이터셋의 경우 약 2천만개 쿼리 예산을 사용하였을 때부터 최적의 정확도로 수렴하였습니다.

Ablation Study

실험 이후, 실험 결과에 얼마나 영향을 미치는지 확인하기 위해 손실 함수의 종류와 손실함수를 계산할 때 사용되는 값을 다르게 하여 Test Accuracy의 변화를 실험하였습니다. 실험 결과는 다음과 같습니다.

Accuracy of Data-free model extractions

위 표에서 각 항목에 해당하는 값들을 정리하면 다음과 같습니다.

방법 손실 함수 사용 값 비고
DFME L1 Loss Logits 제안한 기본 방법
DFME-KL KL Loss Logits -
MAZE - - 다른 논문에서 제안한 방법
Log-Probabilities L1 Loss Softmax 각 모델의 출력값인 softmax를 logit으로 변환하지 않고 그대로 사용

결과를 살펴보면 각 모델의 Logits 값들을 출력값으로 사용하여 손실함수를 L1 Loss로 손실을 계산하였을 때 최적의 성능을 보이는 것을 확인하였습니다.

Test Accuracy for Loss Functions
Norm Gradient form Loss Functions

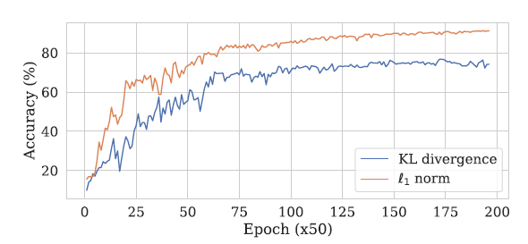
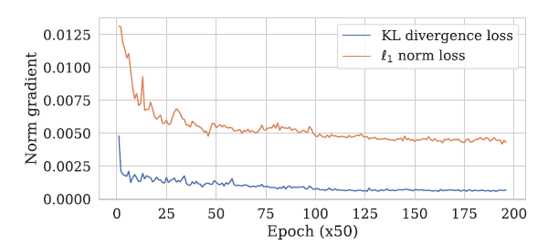
위 결과를 확인해보면, L1 Loss를 사용하였을 때, KL Divergence Loss를 사용하였을 때보다 더 좋은 성능을 보였습니다.

기울기 손실(Gradient Vanishing) 문제도 KL Divergence Loss를 사용하였을 때가 L1 Loss를 사용하였을 때보다 더 확실하게 나타나는 것을 확인하였습니다.

다음 실험에서는 기울기 근사 과정에서, 방향 벡터 \(\mathbf{u}_i\)의 개수 \(m\)값을 어떻게 조정하는 것이 좋을지 확인해보았습니다.

\(m\)값을 크게 설정하면 기울기 근사의 정확도는 올라가지만, 쿼리 복잡도(Query Complexity)가 늘어나 전체 쿼리 예산 중 더 많은 비율이 생성기 학습에 사용되게 됩니다.

쿼리 비율 ( r )은 다음과 같이 계산됩니다.

\[r = \frac{n_S}{n_S + (m+1)n_G}\]

  • \(n_G\): 생성기 학습 반복 수

  • \(n_S\): 학생(Student) 모델 학습 반복 수

  • \(m\): 무작위 방향 수

예시를 들어 설명해보면 \(n_G = 1\), \(n_S = 5\)일 때,

  • \(m = 1\)이면 학생 모델 학습에 71%의 쿼리 예산이 사용됩니다.
  • \(m = 10\)이면 학생 모델 학습에 31%의 쿼리 예산이 사용됩니다.

나머지 쿼리는 더 나은 기울기 추정을 위해 생성기 학습에 사용됩니다.

최적의 \(m\)값을 찾아내기 위해 \(m\)값을 다르게하며 실험을 진행하였습니다. 결과는 다음과 그림과 같습니다.

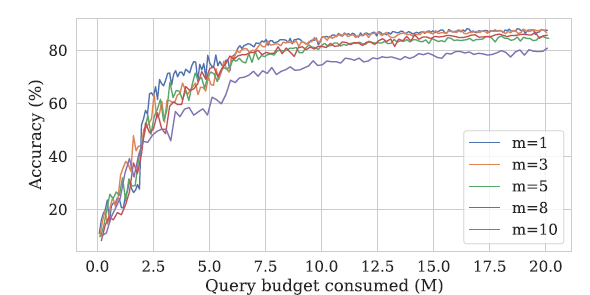
Accuracy of models during training for different gradient approximation steps, m
Minimum queries to reach 85% accuracy for different gradient approximation steps, m

위의 그래프는 \(m\)값에 따른 모델 학습 시 정확도 변화를 나타내고, 표는 \(m\)값에 따른 모델이 85%의 정확도를 처음으로 달성하는데 필요한 최소한의 쿼리 수를 나타냅니다.

표를 보면 \(m\)값이 낮을수록 85%의 정확도를 적은 쿼리 수로 빠르게 달성할 수 있음을 알 수 있습니다.

\(m = 1\)인 경우, 단 하나의 무작위 방향 \(u\)만을 사용하여 경사를 근사합니다. 이 때, 방향이 실제 기울기 벡터의 방향과 다르더라도 기울기 근사 과정에서 부호를 조정하여 \(u\)또는 \(-u\)를 선택함으로써, 항상 손실이 증가하는 방향으로 맞춥니다.

따라서 Student 모델의 학습이 이루어지지 않은 초기 단계의 학습에서는 Student 모델이 Genertor에 강력한 신호를 주지 못하므로\(m = 1\)로 설정하여 Generator의 학습보다 Student의 초기 학습에 힘쓰고, 이후에 모델이 어느정도 학습되면 \(m\)값을 늘리는 방법이 모델을 최적화할 수 있는 가장 좋은 방법입니다.

결론

본 논문에서는 데이터 없는 모델 추출(Data-Free Model Extraction) 기법의 실현 가능하다는 사실과, 피해 모델(victim model)의 정확한 복제본을 생성할 수 있음을 입증하였습니다. 이는 모델 추출 공격이 공개된 모델의 지적 재산권(Intellectual Property)에 심각한 위협이 될 수 있음을 의미합니다.

또한, 향후 연구의 방향으로, 정상 사용자에게 모델의 활용성을 저해하지 않으면서 이러한 공격성 쿼리를 탐지하는 방법을 제안하고 있습니다.