논문명: High Accuracy and High Fidelity Extraction of Neural Networks

저자: Matthew Jagielski, Nicholas Carlini, David Berthelot, Alex Kurakin, and Nicolas Papernot

게재지: In USENIX Security Symposium. USENIX Association, 2020

URL:High Accuracy and High Fidelity Extraction of Neural Networks

서론

모델 추출 공격은 공격자가 원격에 배포된 모델에 대하여 질의(Query) 권한이 있을 때, 질의를 통해 해당 모델의 복제본을 추출하는 행위입니다. 이 공격은 다음 두 지표에서 높은 성능을 목표합니다.

  • 정확도 (Accuracy): 추출 모델이 테스트 분포에 대해 갖는 예측 정확도
  • 충실도 (Fidelity): 추출 모델이 임의의 입력에 대해 원본 모델과 동일하게 예측하는 정도
파랑: 원본 모델, 초록: 높은 충실도, 주황: 높은 정확도

높은 정확도의 모델을 추출하기 위해, 본 논문은 원본 모델을 라벨링 오라클로써 추출 모델을 학습하는 방식을 제안합니다. 학습 기반 방식으로 높은 정확도를 달성할 수 있습니다. 그러나 높은 충실도를 달성하기는 어렵습니다.

이러한 한계를 극복하기 위해, 본 논문은 훈련 없이 원본 모델의 가중치를 추출하는 함수적 동등 (Functionally-equivalent) 방식을 제안합니다. 그리고 실험을 통해 100%에 가까운 충실도를 달성하며, 함수적 동등 방식의 성능을 입증합니다.

사전 지식

배경

기존 연구가 주로 정확도에 초점을 맞췄다면, 이 논문은 충실도 역시 동일하게 중요하다고 봅니다. 추출 모델에서 만든 적대적 예제를 원본 모델에 잘 전이시키려면 두 모델의 충실도가 높아야 하고, 멤버십 추론 역시 피해 모델의 신뢰도를 정밀하게 복제할수록 유리합니다. 또한 기능적으로 동등한 추출이 가능해지면 모델 내부를 분석하여 학습 목표와 상관 없는 속성을 파악할 수 있고, 이를 통해 과잉학습(Overlearning)을 활용할 수 있습니다.

공격 난이도

입력과 출력에 대한 정보만으로 원본 모델과 내부 파라미터가 일치하게 추출 (Exact Extraction) 하기는 현실적으로 어렵습니다. 따라서 공격자의 목표는 달성 난이도에 따라 아래 세 가지로 분류됩니다.

  • 함수적 동등 추출 (Functionally Equivalent Extraction) 모든 입력에 대해 원본 모델과 대체 모델의 출력이 일치하도록 대체 모델을 구성합니다. Exact Extraction 과 달리, 내부 파라미터는 다를 수 있습니다.

  • 충실도 추출 (Fidelity Extraction) 성능 측정용 분포 상에서 두 모델 예측의 유사도를 최대화합니다. 예를 들어 자연 데이터 분포나 적대적 예제가 포함된 분포, 학습 데이터와 비학습 데이터를 섞은 분포를 대상으로 수행됩니다. 함수적 동등 추출은 모든 입력에 대해 일치해야 하지만, 충실도 추출은 주어진 분포 내에서만 일치하면 되기 때문에 난이도가 더 낮습니다.

  • 정확도 추출 (Task Accuracy Extraction) 실제 과제 분포 상에서 예측 정확도를 최대화합니다. 따라서 원본 모델의 오류까지 재현할 필요가 없습니다. 이로 인해 가장 쉬운 목표로 간주됩니다.

학습 기반 추출 공격 (Learning-based Model Extraction)

완전 지도 추출 (Fully-supervised Model Extraction)

공격자는 레이블이 없는 데이터만 갖고 있다고 가정합니다. 대신 원본 모델을 라벨링 오라클로 삼아, 관심 입력들을 질의해 얻은 (입력, 라벨/점수) 쌍으로 추출 모델을 지도 학습합니다.

아래 실험에서는 해당 학습 방식과 실제 학습 데이터로 학습시키는 경우를 비교하여, 완전 지도 추출 공격의 성능을 평가합니다.

완전 지도 추출 성능

본 실험은 공격자가 WSL 오라클(인스타그램 이미지로 학습됨)에 비라벨 ImageNet 데이터를 질의하고, 레이블과 확률을 제공 받는다고 가정합니다. 공격자는 비라벨 ImageNet 데이터와 오라클로부터 받은 레이블로 ResNet-v2-50/200 추출 모델을 지도 학습시킵니다. 비교를 위해 동일한 분량의 ImageNet 데이터와 정답 레이블로 학습한 베이스 라인을 함께 준비합니다.

실제 레이블 vs 오라클 레이블

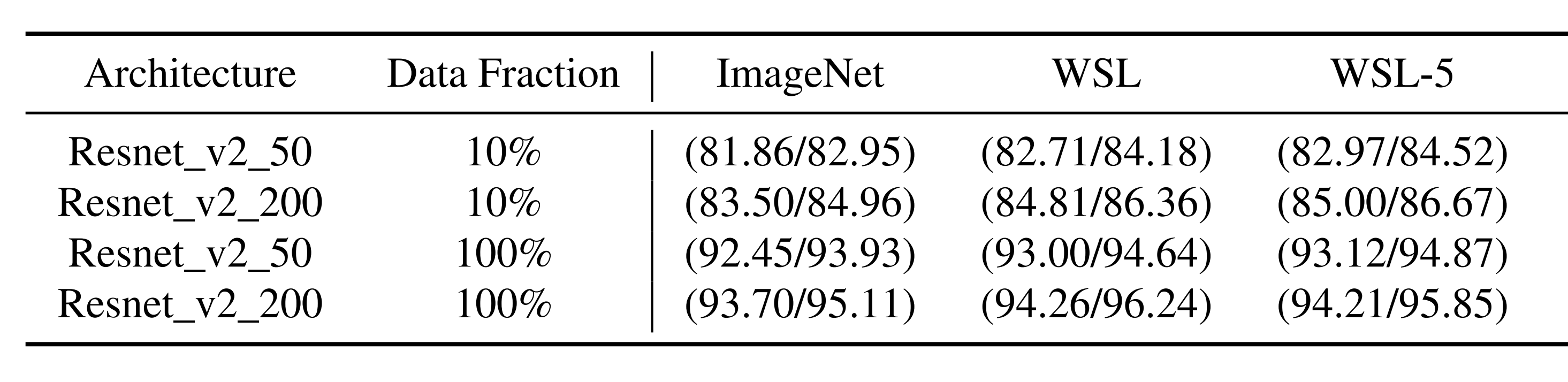
위 실험 결과에서 각 수치는 (Top-5 Accuracy / Top-5 Fidelity)를 의미합니다.

  • Top-5 Accuracy ImageNet 검증 셋에 대해, 추출 모델이 예측한 상위 5개 클래스 중 하나라도 실제 정답 클래스에 포함될 확률

  • Top-5 Fidelity ImageNet 검증 셋에 대해, 오라클의 Top-1 예측 클래스가 추출 모델의 Top-5 예측에 포함될 확률

ImageNet은 베이스 라인, WSL는 오라클이 전체 클래스 확률을 출력하는 경우, WSL-5는 상위 5개 클래스 확률을 출력하는 경우입니다. 그리고 행의 Data Fraction은 공격자가 사용한 ImageNet 비율을 뜻합니다.

관찰 결과, 같은 비율의 데이터를 사용하더라도 오라클의 출력을 활용하는 WSL, WSL-5가 베이스 라인보다 우세합니다. 또한 WSL-5는 WSL과 비슷한 성능을 보이며, 오라클 정보량을 줄여도 베이스 라인 대비 우세한 것을 알 수 있습니다.

오라클 질의 수

학습 기반 추출 공격은 오라클에 질의하여 레이블을 획득해야 합니다. 공격자는 다음 방법들로 오라클 질의 수를 절감할 수 있습니다.

  • 능동 학습 (Active Learning) 데이터 전체에서 정보량이 높은 데이터만 선별해 오라클에 질의하는 기법입니다.

  • 준지도 학습 (Semi-supervised Learning) 라벨된 데이터와 훨씬 더 많은 비라벨 데이터를 함께 활용하는 기법으로, 제한된 질의 예산을 보완하며 모델 성능을 향상시킵니다.

    • 회전 손실 (Rotation Loss) 회전 손실은 이미지 분류 모델에 회전 예측 분류기를 추가하는 준지도 학습 기법입니다. 입력 이미지를 0°, 90°, 180°, 270°로 회전시켜 각도를 예측하도록 학습하며, 이를 통해 객체의 위치, 유형, 자세를 이해하도록 유도합니다. 비라벨 데이터에는 회전 손실을 적용하고, 라벨 데이터에는 기존 분류 손실과 병행하여 모델이 레이블 없이도 유의미한 특징을 학습하도록 합니다.
    • MixMatch MixMatch는 각 비라벨 이미지를 여러 번 증강하고, 증강된 이미지에 대해 모델이 예측한 클래스 확률값을 평균 내어 하나의 가설 레이블(Pseudo-Label)을 생성합니다. 이후 이 가설 레이블이 붙은 이미지들은 MixUp 기법을 통해 소량의 실제 라벨 데이터와 결합되고, 훈련 샘플로 사용됩니다.

회전 손실, MixMatch 성능

회전 손실 (Rot) 성능

위 실험 결과를 보면, 기존 추출 방식에 회전 손실을 추가했을 때 성능이 향상되는 것을 알 수 있습니다. 오라클 질의 수를 줄이는 것이 주요 목표이므로, Data Fraction이 10%인 경우에만 회전 손실 실험을 진행했습니다.

완전 지도(FS) vs MixMatch(MM)

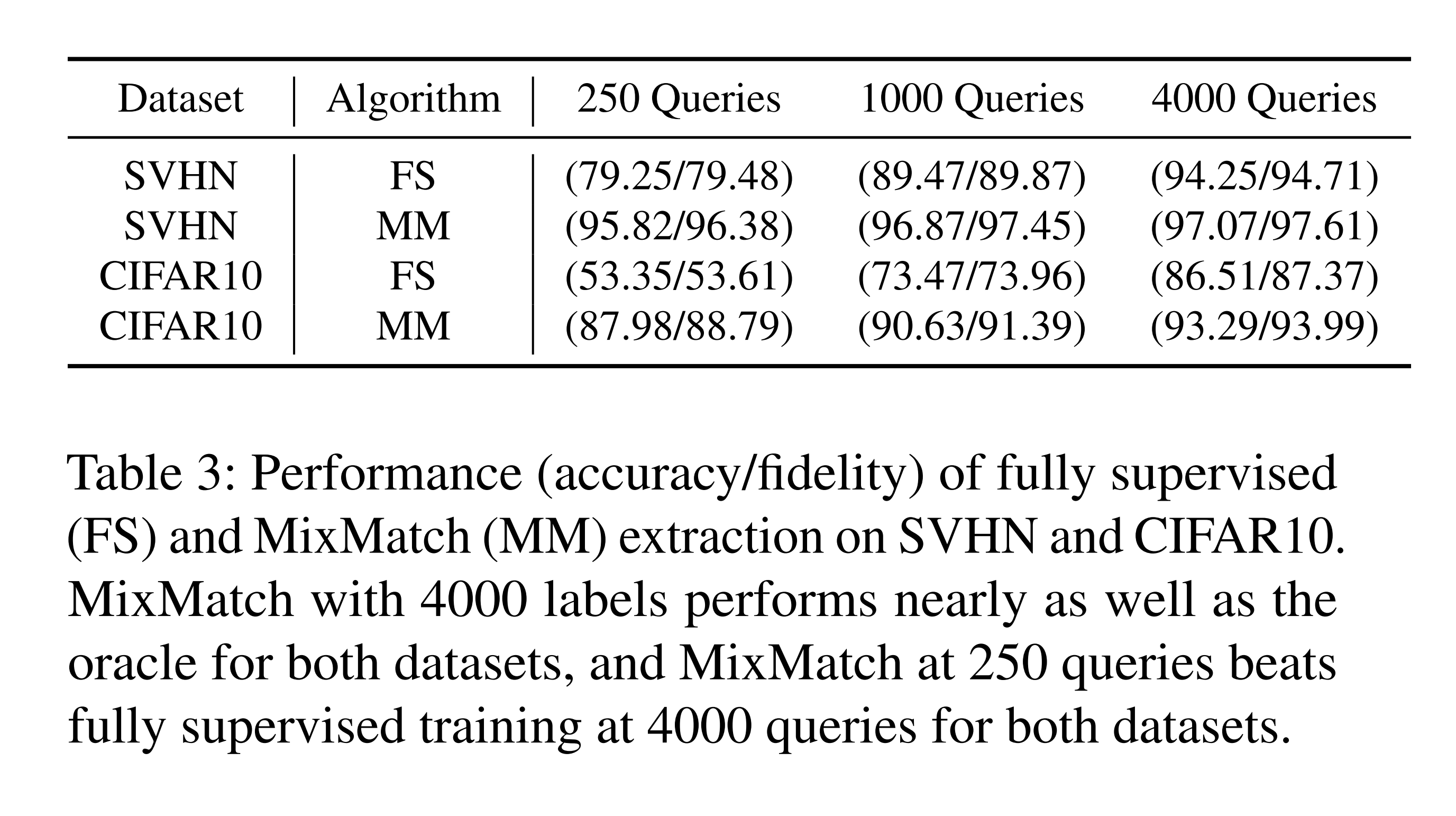
위 실험 결과를 보면, MixMatch가 오라클 질의 250개만으로 오라클 질의 4,000개의 FS(완전 지도) 방식보다 뛰어난 성능을 보여줍니다.

학습 기반 추출 공격 한계

학습 기반 추출 방법은 비결정성(Non-determinism)으로 인해 함수적 동등에 도달하기 어렵습니다. 본 논문은 이러한 비결정성의 이유를 다음 세 가지 요소들로 설명합니다

  1. 모델 파라미터의 무작위 초기화
  2. SGD 미니배치 구성 순서
  3. GPU 계산 자체의 비결정성
비결정성 통제 실험

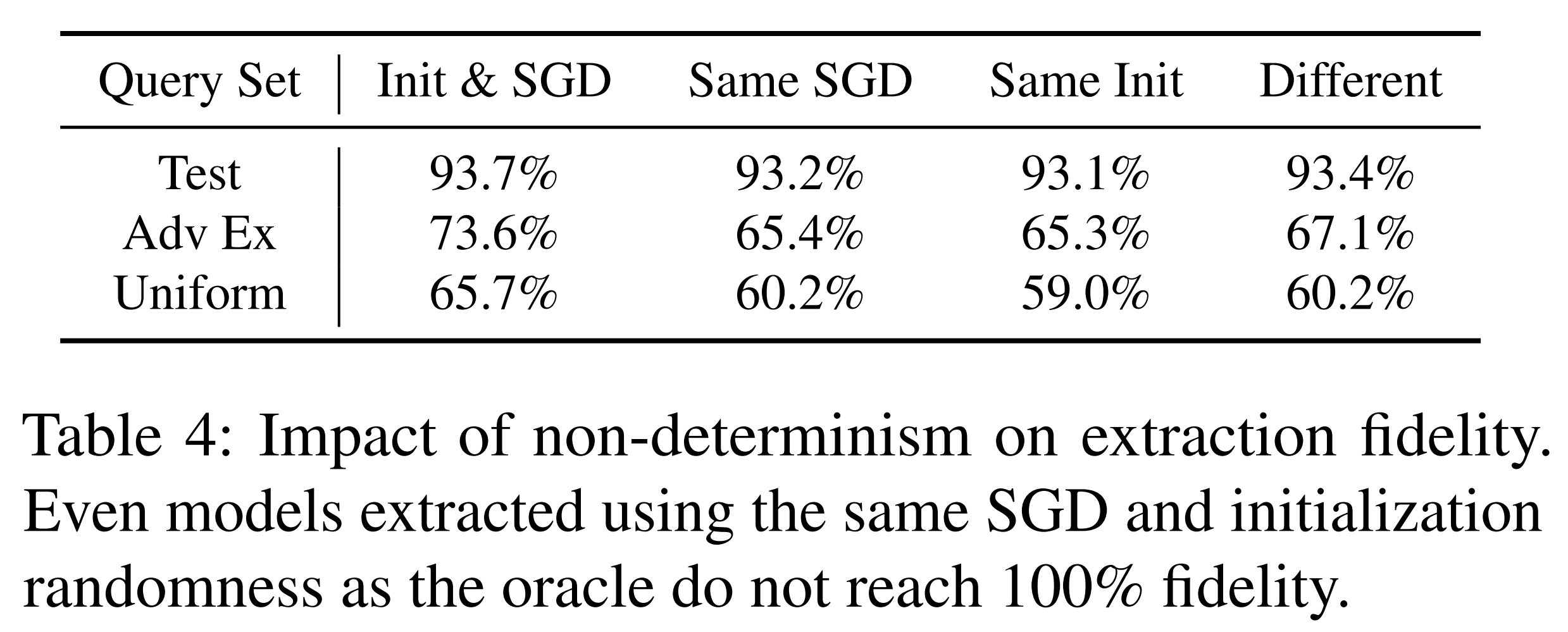
위 실험 결과에서 열은 고정된 변인을, 행은 입력 분포를 의미합니다. 입력 분포는 패션 MNIST의 테스트셋, 오라클 모델에서 생성한 FGSM 적대적 예제, 그리고 입력 공간에서 무작위 샘플링한 데이터로 구성됩니다. 각 요소는 추출 모델에 동일한 입력을 두 번 적용했을 때 두 예측 결과의 일치율, 즉 비결정성의 영향력을 표현하기 위한 수치입니다.

그 결과, 모든 통제 가능한 변인을 고정한 경우에도 일치율 최대 93.7%로 100%를 달성하지 못했습니다. 이는 학습 기반 접근법의 본질적인 한계를 보여주며, 이에 따라 함수적 동등을 달성하려면 다른 추출 방법이 필요하다는 결론을 내릴 수 있습니다.

함수적 동등 추출 공격 (Functionally Equivalent Extraction)

요약

함수적 동등 추출은 원본 모델의 가중치를 직접 복원하여 함수적 동등을 달성하는 공격 기법입니다. 본 연구에서는 단층 ReLU 신경망에서 동작하도록 설계되었으며, ReLU 층의 활성화 경계 정보를 바탕으로 ReLU 직전 은닉층과 직후 은닉층의 가중치를 추적합니다. 이 과정을 아래에서 5단계로 설명합니다.

단층 ReLU 신경망 내부 차원
ReLU 직전 은닉층의 활성화 경계선
\[O_L(x)=A^{(1)}\,\mathrm{ReLU}(A^{(0)}x+B^{(0)})+B^{(1)}\]

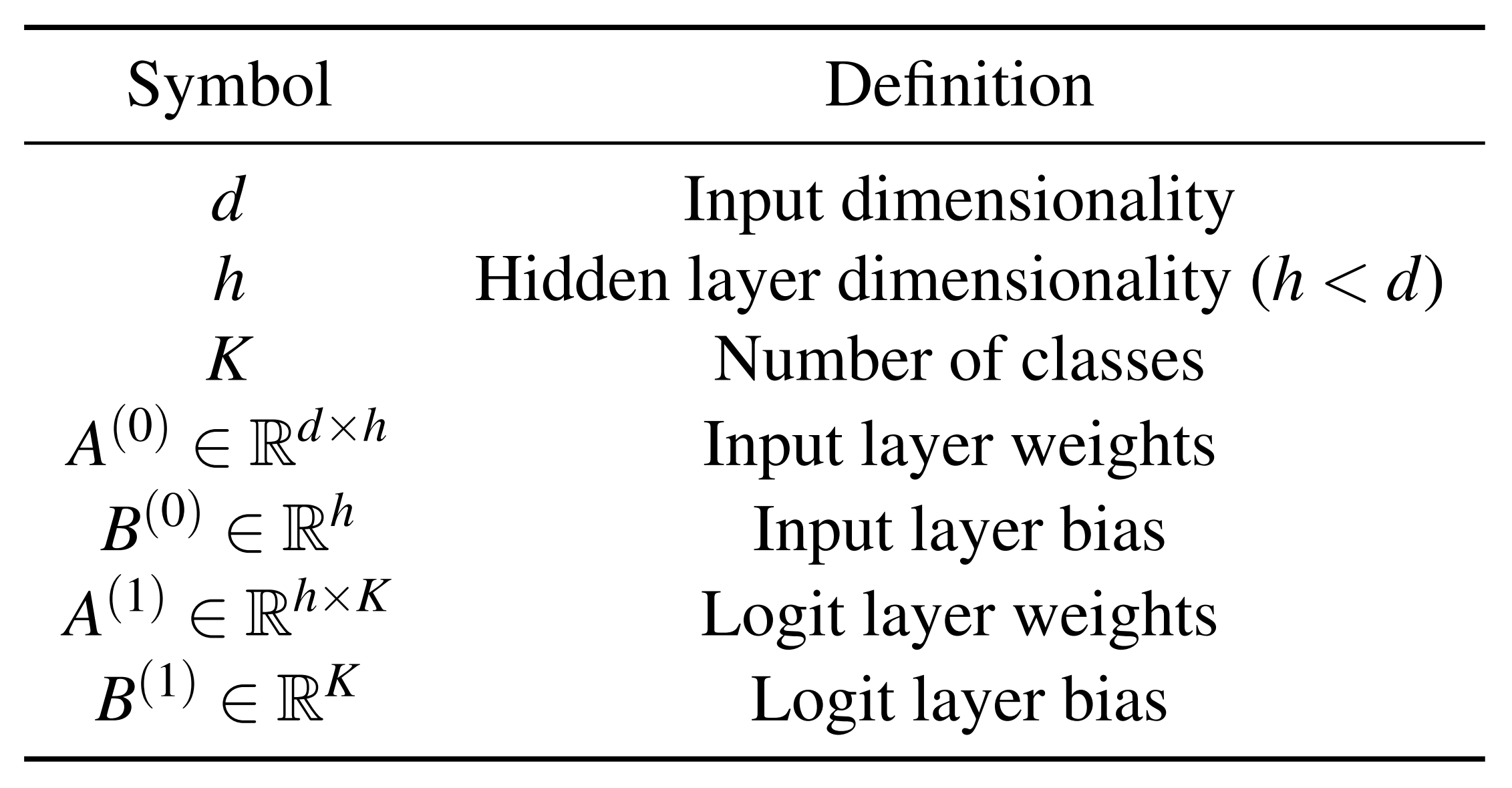
\(O_L(x)\) 는 오라클 모델에 \(x(t) \in \mathbb{R}^d\) 를 입력했을 때의 로짓입니다.

  • \(A^{(0)}\): 입력에서 ReLU 직전 은닉층으로 갈 때의 가중치 행렬 \(\in \mathbb{R}^{d\times h}\)
  • \(A^{(1)}\): ReLU 직후 은닉층에서 로짓층으로 갈 때의 가중치 행렬 \(\in \mathbb{R}^{h\times K}\)

Table 5는 입력, 출력 차원을 행렬곱 형태로 맞추기 위해 가중치 행렬의 차원을 전치한 상태입니다. 따라서 실제 \(O_L\) 수식 상 \(A\)의 행 벡터의 차원은 다음과 같습니다.

  • \(A^{(0)}_i\): \(A^{(0)}\) 의 \(i\) 번째 가중치 행 벡터 \(\in \mathbb{R}^{d}\)
  • \(A^{(1)}_i\): \(A^{(1)}\) 의 \(i\) 번째 가중치 행 벡터 \(\in \mathbb{R}^{k}\)

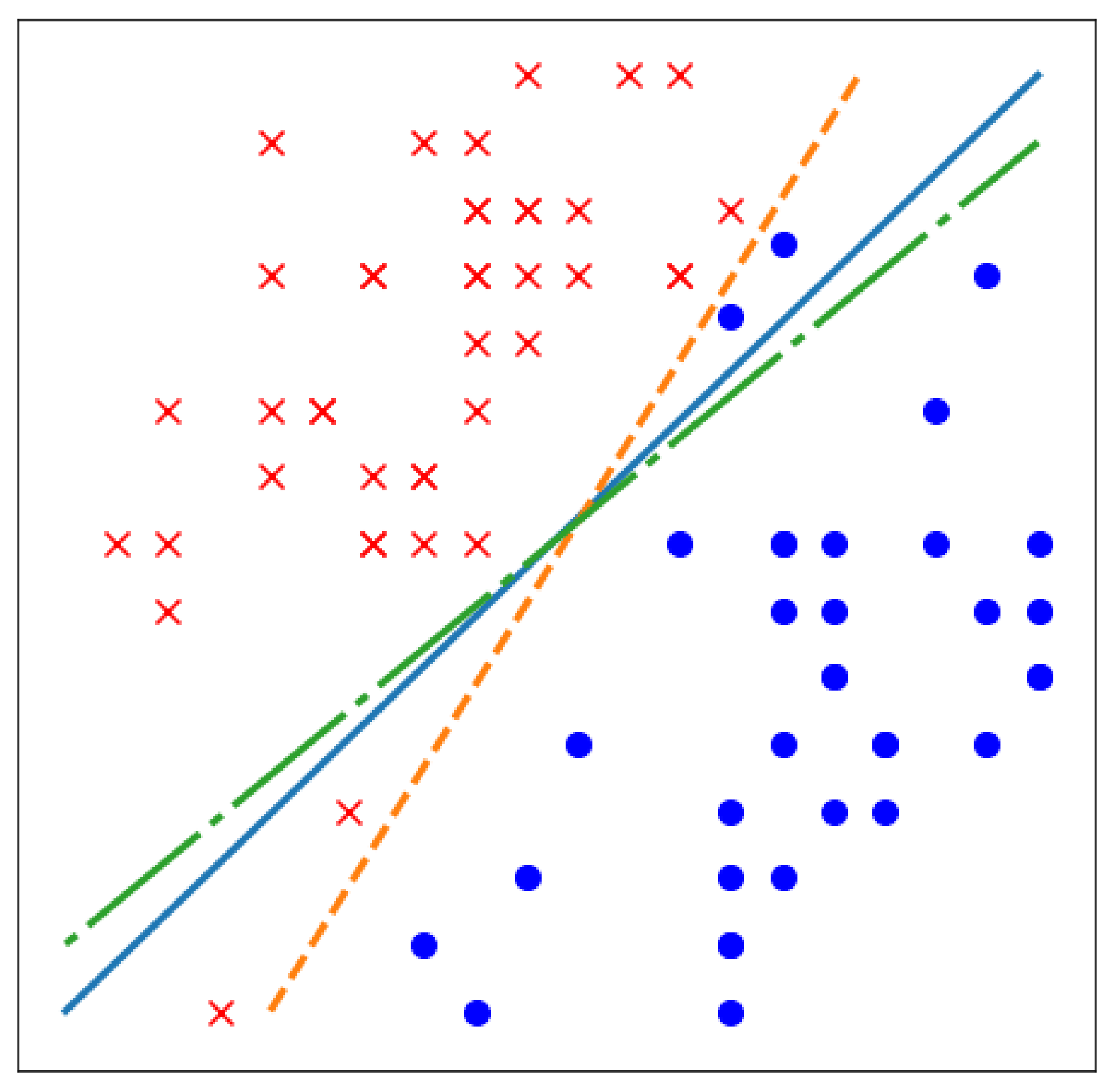
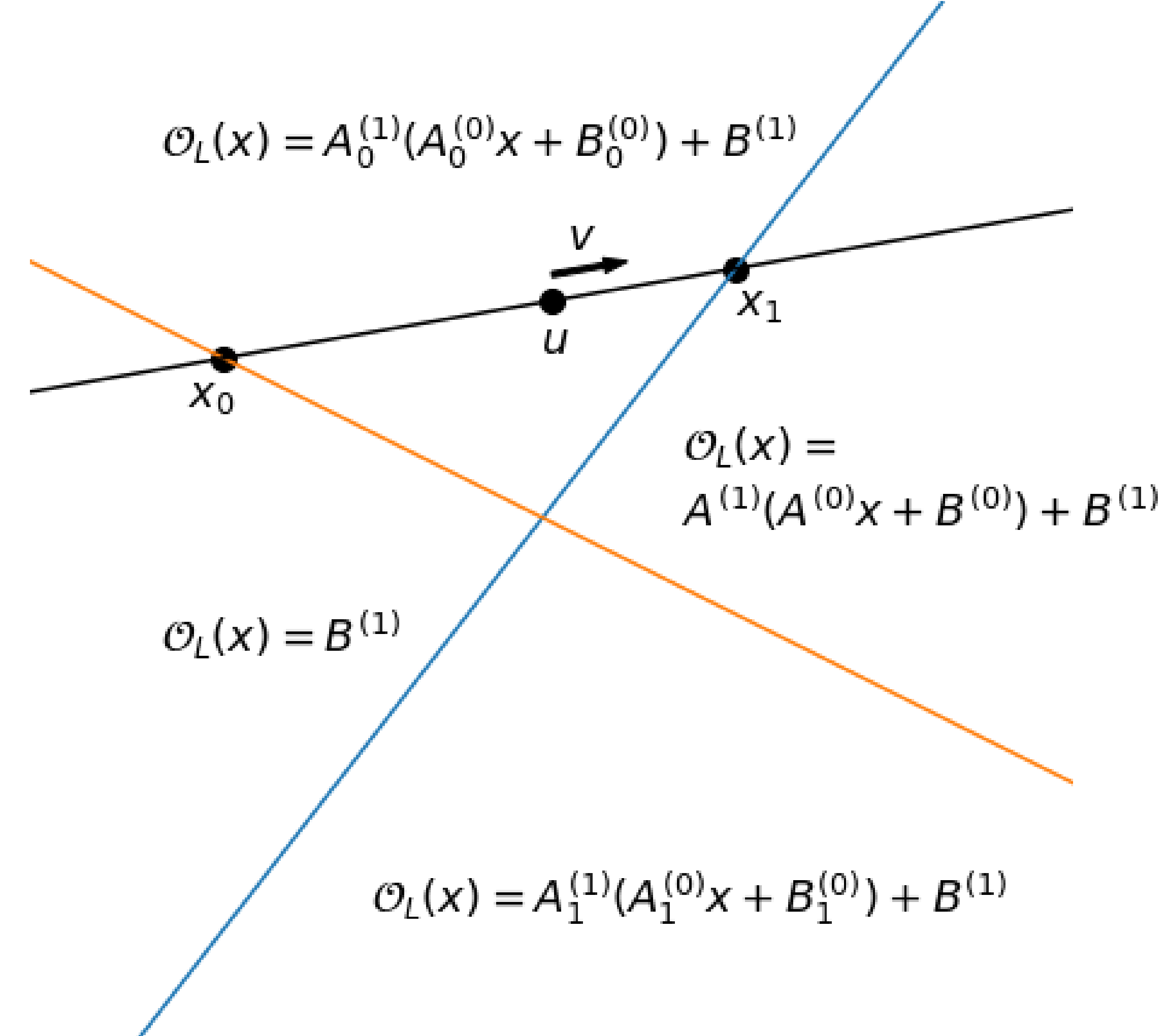
그리고 ReLU 직전 은닉층의 입력 \(x\)에 대하여, Figure 2의 주황 직선과 파란 직선은 각각 \(A^{(0)}_{0}x + B^{(0)}_{0}=0\), \(A^{(0)}_{1}x + B^{(0)}_{1}=0\) 이 되는 경계선을 의미합니다.

공격자는 임의의 벡터 \(u, v \in \mathbb{R}^d\) 를 샘플링하여, 임의의 직선 \(x(t)=u+tv\) 를 제작합니다. 그리고 \(t\) 지점에서 \(x(t)\) 값을 \(O_L(x)\) 에 입력하여, 그 결과값을 \(L(t)=O_L​(u+tv)\) 라고 정의합니다. 이처럼 \(L(t)\) 는 ReLU 층의 로짓이기 때문에, Figure 2에서의 주황 직선과 파란 직선을 경계로 기울기가 달라지는 구간별 선형 함수입니다.

Figure 2에서 주황 직선 위는 \(A^{(0)}_{0}x + B^{(0)}_{0}>0\), 파란 직선 오른쪽은 \(A^{(0)}_{1}x + B^{(0)}_{1}>0\) 을 의미합니다. 그 결과, 해당 영역들만 ReLU 층의 출력값이 0보다 크고, 이를 표시한 내용이 Figure 2의 \(O_L(x)\) 수식입니다.

공격자는 \(t\) 를 조정하며 \(L(t)\) 가 미분 불가능한 지점을 찾고, 해당 지점을 Critical point로 간주합니다.

미분 불가능한 지점

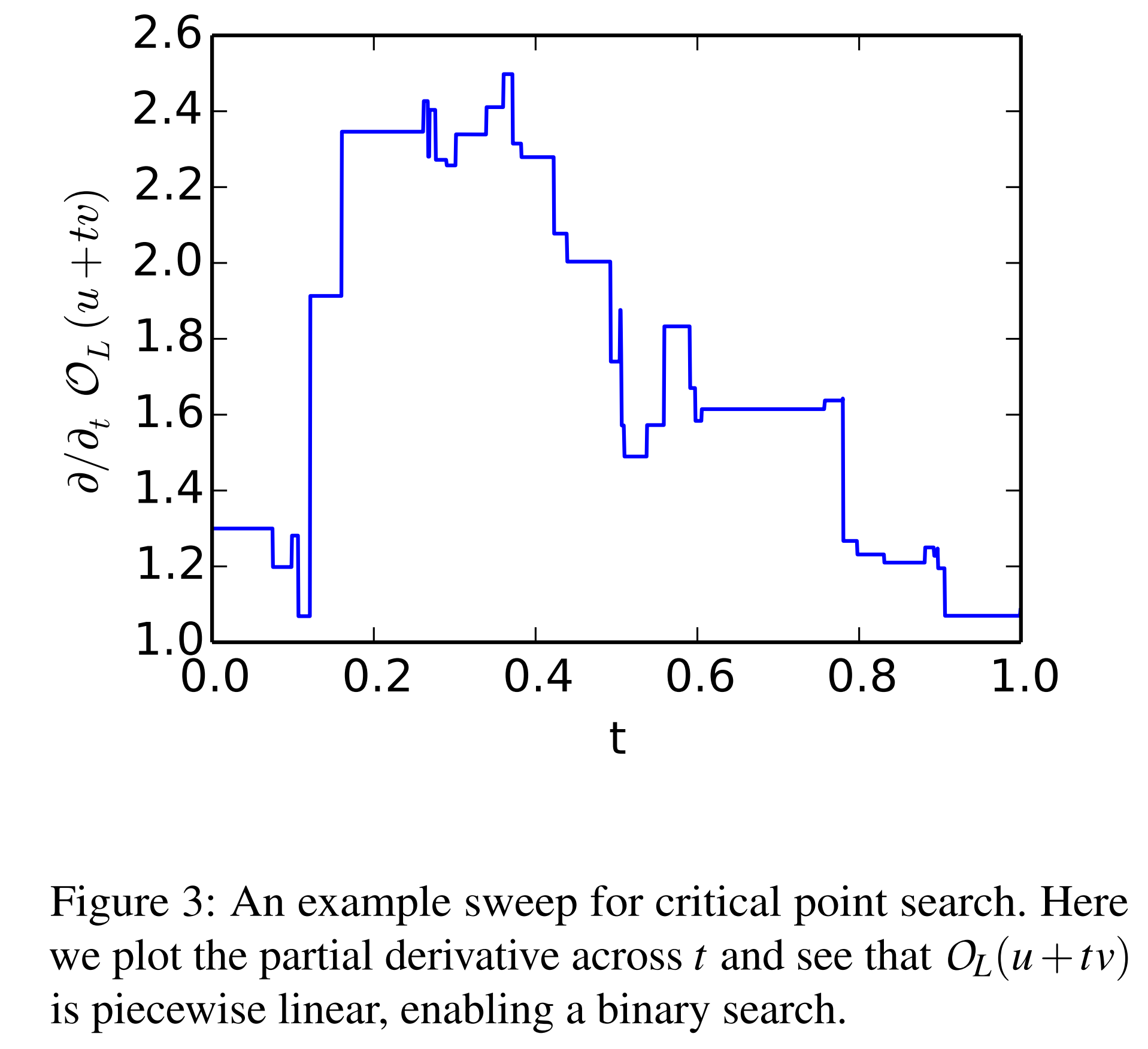
2. Absolute Value Recovery

이전 단계에서 공격자는 \(h\) 개의 경계 \(A^{(0)}_{i}x + B^{(0)}_{i}=0\) 위에 존재하는 Critical point \(x_i\) 들을 확보했습니다. 이제 이 \(h\) 개의 \(x_i\) 를 이용하여, \(A^{(0)}\) 에 접근할 수 있습니다.

\[\frac{\partial^2 O_L}{\partial e_j^2} \Big|_{x_i} = \frac{\partial O_L}{\partial e_j} \Big|_{x_i + c e_j} - \frac{\partial O_L}{\partial e_j} \Big|_{x_i - c e_j} = \pm \left( A^{(0)}_{ji} A^{(1)}_i \right)\]

위 수식처럼 입력 공간 내 임의의 방향 \(e_j \in \mathbb{R}^d\)에 대해 \(x_i\) 근방의 이계도를 유한차분으로 계산하면, \(A^{(0)}\) 의 좌표와 \(A^{(1)}\) 의 행 간 곱으로 정리됩니다.

그리고 각 \(x_i\) 마다 방향 \(e_j\) 를 바꿔가며 $$ A^{(0)}_{ji} A^{(1)}_i \(를 구한 뒤, 서로 나누면\)\big \tfrac{A^{(0)}{1i}}{A^{(0)}{ki}}\big \(처럼 같은\)i$$ 행에서의 좌표 간 비율이 나옵니다.

이렇게 해서 각 행 벡터 \(A^{(0)}_i\) 마다 부호만 제외하고 모두 복원합니다.

3. Weight Sign Recovery

이제 각 행 벡터 \(A^{(0)}_i\) 의 부호를 정해야 합니다.

Critical point \(x_i\) 에서 두 방향의 합 \((e_j+e_k)\) 으로의 이계도를 유한차분으로 계산하면, 아래 수식처럼 정리됩니다.

\[\left.\frac{\partial^2 O_L}{\partial (e_j+e_k)^2}\right|_{x_i} \!=\ \pm\!\big(A^{(0)}_{ji}A^{(1)}_i \ \pm\ A^{(0)}_{ki}A^{(1)}_i\big)\]

이때 우변의 두 항이 상쇄되면 \(A^{(0)}_{ji}\)와 \(A^{(0)}_{ki}\) 는 반대 부호, 증폭되면 같은 부호입니다. 이것을 모든 방향끼리 계산하면 \(A^{(0)}\) 의 모든 행 벡터 간 상대 부호는 결정되지만, 실제 부호는 알 수 없습니다.

4. Global Sign Recovery

지금까지 복원한 \(\hat A^{(0)}\) 의 모든 행 벡터의 실제 부호를 알게 된다면, \(A^{(0)}\) 가 갖는 \(h\) 개의 경계선에 대하여, 경계선 기준으로 어느 방향이 \(A^{(0)}_{i}x + B^{(0)}_{i}≥0\) 인지 알 수 있습니다.

이를 위해 먼저 \(\hat A^{(0)} z=\mathbf{0}\) 를 만족하는 영공간 벡터 \(z\) 를 설정합니다. 그리고 각 \(i\) 마다 \(v_i A^{(0)}=e_i\) 를 만족시키는 \(v_i\) 를 찾습니다.

이후 \(O_L(z), \ O_L(z\!+\!v_i), \ O_L(z\!-\!v_i)\) 를 비교하며, 각 행 벡터의 부호를 판정합니다. 같은 방식으로 \(B^{(0)}\) 도 부호까지 복원합니다.

비교 항목 동일 여부 \(A^{(0)}_i\!\cdot v_i\)
\(O_L(z+v_i), O_L(z)\) 같으면 \(< 0\)
\(O_L(z-v_i), O_L(z)\) 같으면 \(> 0\)

5. Last Layer Extraction

\(A^{(0)}\), \(B^{(0)}\) 를 다 복원했습니다. 그리고 \(h\) 개의 \(x_i\) 도 확보했습니다.

이제 각 \(x_i\) 를 \(O_L(x)=A^{(1)}\,\mathrm{ReLU}(A^{(0)}x+B^{(0)})+B^{(1)}\) 에 대입하면, 최소제곱법으로 \(A^{(1)}\), \(B^{(1)}\) 를 복원할 수 있습니다.

성능 실험

오라클의 \(A^{(0)}\), \(A^{(1)}\) 뉴런 개수는 각각 16∼512개이며, MNIST와 CIFAR-10으로 학습되었습니다.

함수적 동등 추출 공격

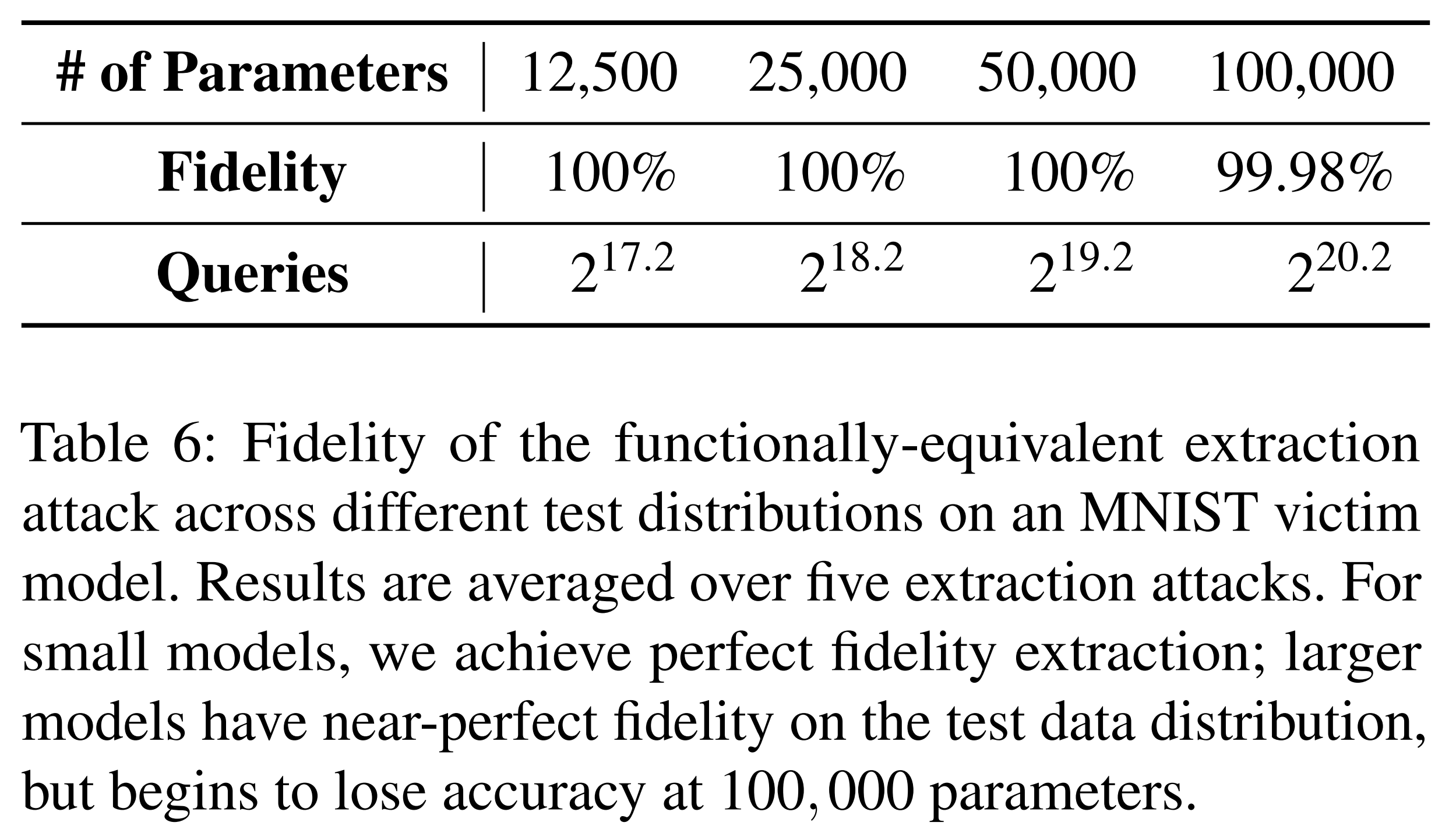
위 실험 결과는 MNIST로 학습한 오라클에 대한 함수적 동등 추출 공격의 성능입니다. 오라클 질의 수가 많지만, 충실도가 100%에 수렴하는 모습을 보입니다.

CIFAR-10에 대해서는 모델 파라미터 수가 200,000개 이하일 때 100%의 충실도를 달성했습니다.

한계

본 연구에서 제안한 함수적 동등 추출 공격은 은닉층 2개만 전제하고 진행했기 때문에 더 깊은 모델에 대해 적용하기 어려움이 있습니다. 그리고 깊은 모델에서는 Critical point를 찾더라도, 그게 어떤 층에서의 지점인지 판별하기 어렵습니다. 설령 층을 알더라도, 모델이 깊은 탓에 뉴런에 직접적으로 접근하기 어렵습니다. 마지막으로 작은 추출 오차가 층마다 누적되면, 전체 오차가 증폭되어 가중치 복원 정확도가 크게 저하됩니다.

하이브리드 전략

요약

학습 기반의 추출 공격의 질의 효율성과 함수적 동등 추출 공격의 높은 충실도를 연속선상에서 섞어서 양쪽의 장점을 취하는 전략입니다.

학습 기반 추출 공격과 Gradient Matching

기존의 학습 기반 추출은 오라클과 추출 모델 \(f\)의 출력만 맞추는 데 초점을 두었습니다. 그러나 Gradient Matching 방식은 해당 출력뿐만 아니라, 입력에 대한 기울기도 함께 맞추도록 학습을 진행합니다. 즉, 공격자는 오라클에 질의할 때 단순히 출력값만 얻는 것이 아니라, 입력 그래디언트 \(\nabla_x O(x)\) 또한 확인할 수 있어야 합니다. 이 전략은 충실도를 개선할 수 있으며, 이를 위해 아래 목적식을 최소화합니다.

\[\sum_{i=1}^{n}\underbrace{H\!\big(O(x_i),\,f(x_i)\big)}_{\text{출력(로짓/확률) 일치}} \;+\; \alpha\,\underbrace{\big\|\nabla_x O(x_i)-\nabla_x f(x_i)\big\|_2^2}_{\text{입력 기울기 일치}}\]

위 수식에서 \(H\)는 교차엔트로피입니다. Fashion-MNIST에서 실험한 결과, 충실도가 95%에서 96.5%로 소폭 개선되었습니다.

오차 보정 학습 (Error Recovery through Learning)

함수적 동등 추출 공격은 이론적으로는 완벽하게 작동하지만, 실체 계산 시 오차가 누적되는 문제가 발생합니다. 특히 \(A^{(0)}\), \(B^{(0)}\) 을 복원할 때 아주 작은 오차가 포함되면, 그 뒤 층으로 갈수록 Bias 항의 오차가 증폭되어 큰 모델일수록 최종 충실도가 크게 떨어집니다.

이를 해결하기 위해, 본 연구는 \(\hat A^{(0)}\), \(\hat B^{(0)}\) 을 초기값으로 두고, 다른 파라미터들을 경사하강법으로 학습시켜서 오차를 보정하는 방식을 제안합니다.

\[\mathbb{E}_{x \in \mathcal{D}} \left\| f_\theta(x) - W_1 \,\mathrm{ReLU}\!\big(\hat{A}^{(0)} x + \hat{B}^{(0)} + W_0\big) + W_2 \right\|\]
  • \(f_\theta(x)\): 오라클 모델의 출력
  • \(\hat{A}^{(0)}, \hat{B}^{(0)}\): 함수적 동등 추출로 얻은 근사치
  • \(W_0, W_1, W_2\): 보정 학습을 위해 새로 도입한 파라미터들
    • \(W_0\): \(B^{(0)}\)를 대신하는 보정항
    • \(W_1\): \(A^{(1)}\)를 보정하는 항
    • \(W_2\): \(B^{(1)}\)를 보정하는 항

위 과정을 통해 초기 추출 단계에서 발생한 작은 오차들이 보정되고, 추출 모델의 충실도가 향상됩니다.

함수적 동등 추출 공격

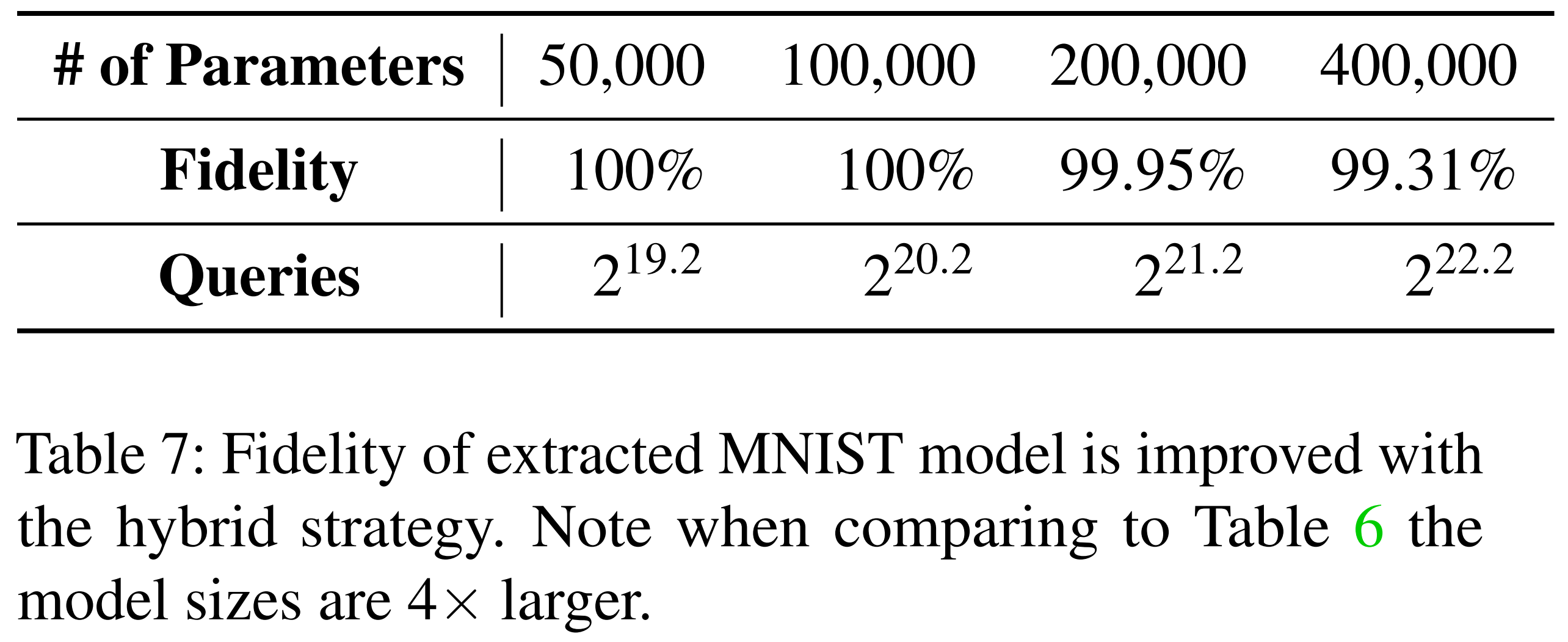
위 표는 함수적 동등 추출만 수행한 결과로, 이미 높은 충실도를 보여줍니다. 이후, 같은 추출 모델에 대해 오차 보정 학습을 추가적으로 적용했습니다.

함수적 동등 추출 공격 & 오차 보정 학습

그 결과, 오차 보정 학습을 마친 추출 모델에서 생성한 적대적 예제들이 오라클에도 100% 전이됨을 확인할 수 있습니다.

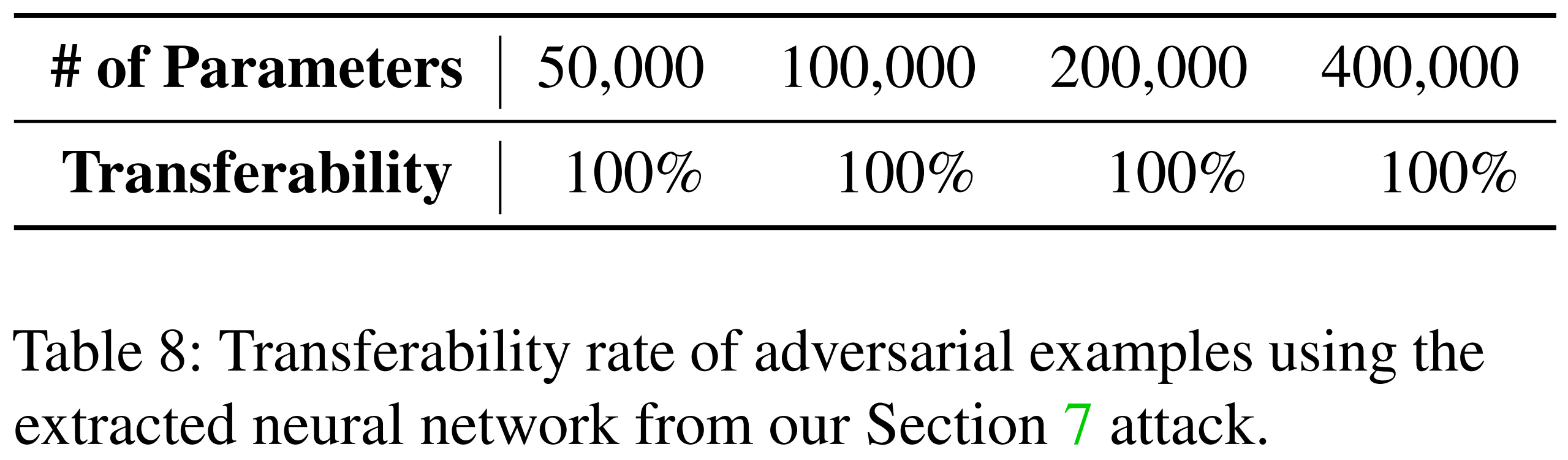
결론

본 논문은 단층 ReLU 신경망을 대상으로, 오라클 질의만으로 내부 가중치와 편향을 복원할 수 있는 새로운 추출 공격 기법을 제안합니다. 이 공격은 ReLU의 비선형 경계 특성을 활용하여 Critical point를 찾아내고, 이를 통해 모델 구조를 직접적으로 역추적합니다. 그 결과, 기존의 학습 기반 추출 방식보다 훨씬 높은 충실도를 달성하였으며, 작은 모델에서는 거의 완벽한 함수적 동등성을 달성했습니다. 또한 하이브리드 전략을 결합할 경우, 모델 크기가 커지더라도 충실도 저하를 완화할 수 있음을 실험으로 확인했습니다. 비록 다층 신경망이나 더 복잡한 구조로의 확장은 한계가 있지만, 본 연구는 함수적으로 동등한 모델 추출이 현실적으로 가능하다는 점을 시사합니다.