논문명: Practical Black-Box Attacks against Machine Learning

저자: N. Papernot, P. McDaniel, I. Goodfellow, S. Jha, Z. B. Celik, and A. Swami

게재지: Proceedings of ACM ASIACCS, 2017

URL:Practical Black-Box Attacks against Machine Learning

서론

기존의 적대적 예제(Adversarial example) 공격은 모델의 내부 구조나 학습 데이터에 대한 정보에 의존한다는 한계를 가지고 있습니다. 본 논문은 이러한 한계를 극복하고, 해당 정보를 모르는 블랙 박스 환경에서도 작동하는 공격 기법을 제안합니다.

본 논문에서 공격자는 모델의 출력 레이블만 관측할 수 있다는 가정 하에, DNN을 포함한 다양한 모델에 대해 공격을 수행합니다. 공격자는 원본 모델에 질의(Query)하여 레이블을 획득하고, Jacobian 기반의 합성 샘플을 생성하여 대체 모델을 학습시킵니다. 이후 대체 모델을 이용해 생성한 적대적 예제가 원본 모델에도 전이되는지를 실험으로 검증합니다.

실험 결과, MetaMind의 원격 DNN에서 84.24%의 오분류율을 보였고, Amazon, Google의 모델에서도 각각 96.19%, 88.94%의 오분류율을 보였습니다. 이를 통해, 출력 레이블만을 활용한 질의로 원본 모델의 결정 경계를 효과적으로 근사하는 대체 모델을 학습할 수 있음을 입증합니다.

본론

대체 모델 학습 과정

대체 모델 학습 과정

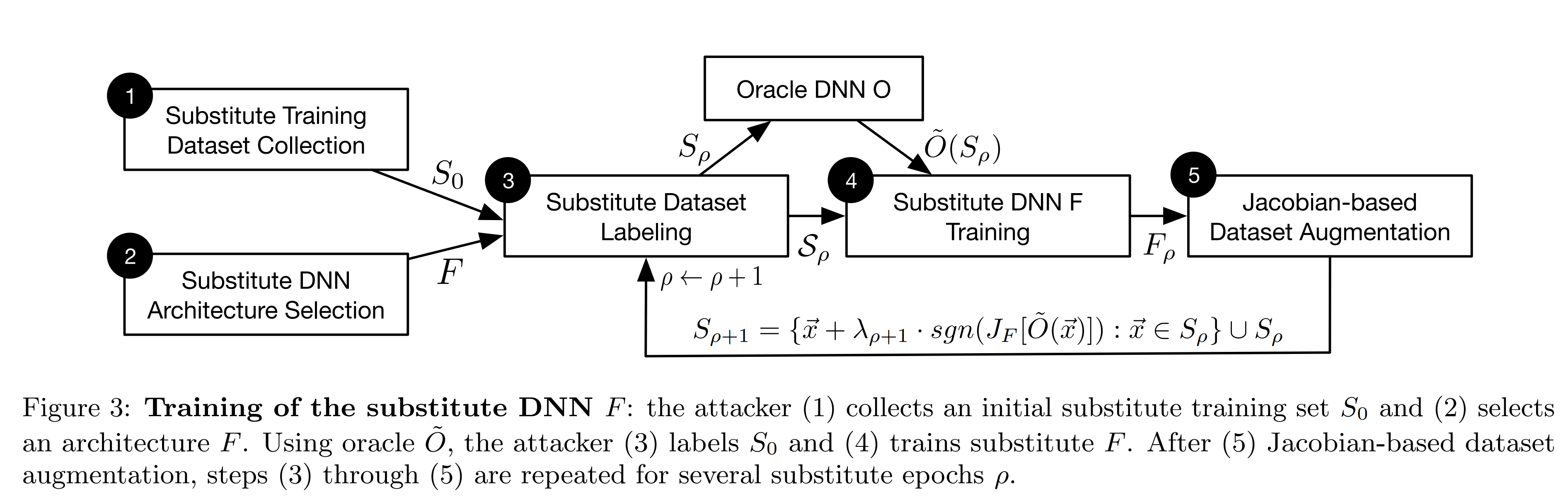
1. 초기 샘플 공격자는 입력 도메인을 대표하는 작은 초기 샘플 \(S_0\) 을 수집합니다.

2. 대체 모델 구조 공격자는 입출력 데이터의 형태를 바탕으로 대체 모델 \(F\) 의 구조를 선택합니다.

3. 데이터셋 제작 현재 학습 집합 \(S_\rho\) 를 오라클 \(O\)에 입력하여 레이블 \(\tilde{O}(S_\rho)\) 을 획득합니다. 그리고 현재 학습 집합과 레이블로 데이터셋 \(D\) 를 제작합니다.

4. 대체 모델 학습 데이터셋으로 대체 모델을 학습하여 \(F_\rho\) 를 생성합니다.

5. 합성 샘플 합성 샘플은 대체 모델이 오라클의 결정 경계를 더욱 잘 근사하도록 돕는 학습 데이터입니다. 공격자는 오라클의 출력 결과를 학습 데이터로 활용한 \(F\) 의 출력이 어떤 방향으로 민감하게 바뀌는지 Jacobian 행렬로 계산합니다. 그리고 그 방향을 따라 데이터셋을 변형시켜 합성 샘플을 제작하고, 이전 단계의 학습 샘플 집합 \(S_\rho\) 에 추가하여 \(S_{\rho+1}\) 를 구성합니다. 이후 3단계부터 반복합니다.

3~5단계를 반복하여 대체 모델을 재학습시킨 후, 공격자는 대체 모델을 활용하여 공격용 적대적 예제를 제작합니다. 본 논문에서는 FGSM, Papernot 알고리즘으로 제작합니다.

FGSM

FGSM(Fast Gradient Sign Method)은 비용함수의 입력 방향에 대한 그래디언트 부호를 따라 입력 데이터를 변형합니다.

\[\vec{x}^{*}=\vec{x}+\delta_{\vec{x}}\] \[\vec{x}^{*}=\vec{x}+\varepsilon\,\operatorname{sgn}\!\big(\nabla_{\vec{x}}c(F,\vec{x},y)\big)\]

FGSM은 입력 데이터를 빠르게 변형할 수 있으며, 변형된 데이터는 적대적 예제로써 모델의 오분류를 유도합니다. 𝜀을 키울수록 오분류 가능성이 높아지지만, 그만큼 사람의 눈으로도 알아채기 쉬워집니다.

Papernot 알고리즘

Papernot 알고리즘은 기존 FGSM 방식과 차이점을 가집니다. FGSM은 입력 데이터의 모든 성분을 동일한 크기로 변형하여 정답 클래스로의 분류를 피할 수 있도록 설계되었습니다. 그러나 이로 인해 특정 클래스로의 오분류를 유도하는 데는 한계가 있습니다.

반면, Papernot 알고리즘은 입력 데이터에서 일부 성분만 선별해 변형하기 때문에, 모든 클래스의 샘플을 임의의 목표 클래스 𝑡로 오분류시키는 데에 적합합니다. 이를 위해 입력 데이터의 각 성분이 가진 Saliency value를 기준으로 각 성분의 변형 여부를 결정합니다. 목표 오분류 클래스가 𝑡일 때, \(i\) 번째 성분에 대한 Saliency value는 아래의 수식으로 계산됩니다.

\[S(\vec{x}, t)[i]= \begin{cases} 0 \ \ \ \ \ \text{if} \ \ \displaystyle \frac{\partial F_t}{\partial \vec{x}_i}(\vec{x})<0 \ \text{or}\ \displaystyle\sum_{j\ne t}\frac{\partial F_j}{\partial \vec{x}_i}(\vec{x})>0\\[10pt] \displaystyle \frac{\partial F_t}{\partial \vec{x}_i}(\vec{x})\,\left|\sum_{j\ne t}\frac{\partial F_j}{\partial \vec{x}_i}(\vec{x})\right| \ \ \ \ \ \ \ \ \ \ \ \ \text{otherwise} \end{cases}\]

Saliency value가 0인 입력 성분은 변형 대상에서 제외됩니다. 특정 입력 성분을 증가시킬수록 목표 클래스 𝑡로의 출력이 감소하거나, 목표 클래스가 아닌 𝑗로의 출력이 증가하는 경우가 이에 해당합니다.

반대로, 특정 입력 성분을 증가시킬수록 목표 클래스 𝑡로의 출력이 증가하는 경우나, 목표 클래스가 아닌 𝑗로의 출력이 감소하는 경우에는 그 크기에 따라 Saliency value가 결정됩니다.

Saliency value가 큰 입력 성분일수록, 변형했을 때 목표 클래스 𝑡로의 오분류 가능성이 커집니다. 따라서 Saliency value를 내림차순으로 정렬하고, 값이 큰 성분부터 순차적으로 변형하여 적대적 예제를 생성합니다. 선택된 각 성분에 적용되는 변형 크기 \(\delta_{\vec{x}}\) 는 후속 실험에서 \(\varepsilon\) 으로 설정됩니다.

\[\vec{x}^{*}=\vec{x}+\delta_{\vec{x}}\]

실험

실험 환경

MNIST 데이터에 대하여 실험을 진행하고, MetaMind의 DNN API를 오라클로 사용합니다.

대체 모델의 분류 성능

본 논문은 공격자가 오라클의 학습 데이터에 접근할 수 없다는 전제를 기반으로 합니다. 따라서 공격자는 수기 작성 데이터로 학습한 대체 모델과 실제 학습 데이터로 학습한 대체 모델 성능이 유사한지 확인해야 합니다. 이를 검증하기 위해, DNN 대체 모델의 초기 학습 샘플로 수기 작성 숫자 이미지 100장과 MNIST의 테스트셋 150장을 각각 사용해 성능을 비교합니다.

초기 학습 샘플 비교

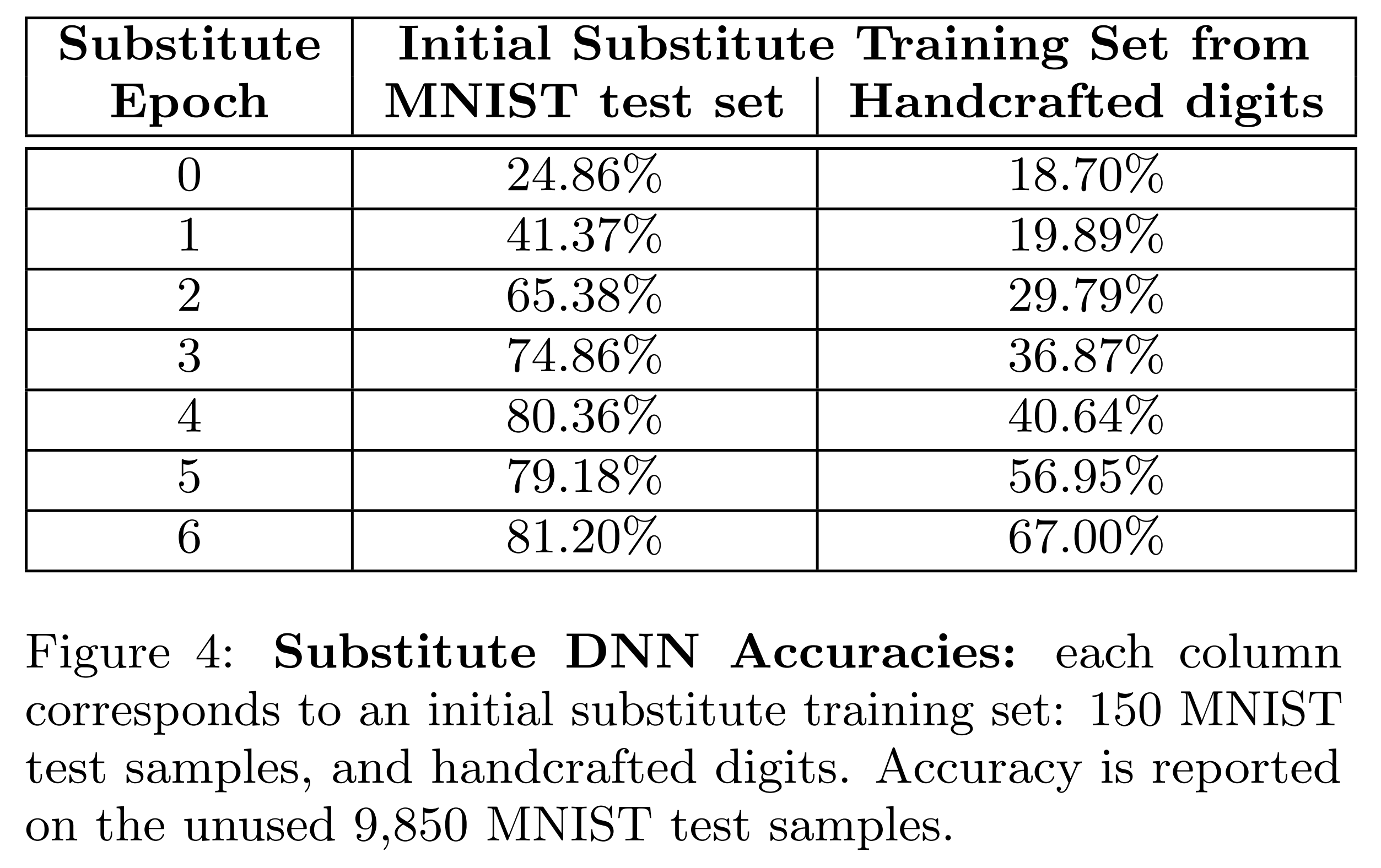
위 결과는 각 대체 모델에 대하여 MNIST의 테스트셋을 입력했을 때의 정확도입니다. 수기 작성 데이터를 사용한 경우의 정확도가 67%로 MNIST의 학습 데이터를 사용한 경우보다 낮습니다.

그러나 본 실험의 주요 목표는 대체 모델의 정확도를 높이는 게 아니라, 대체 모델이 원본 모델의 결정 경계를 잘 근사하는지 확인하는 데 있습니다. 이에 대한 검증은 다음 실험에서 이어집니다.

대체 모델의 결정 경계 근사 성능

위 실험에 사용된 두 가지 대체 모델에 대하여 FGSM으로 적대적 예제를 생성합니다. 그리고 이를 대체 모델과 원본 모델에 각각 입력하여 오분류 성공 여부를 확인합니다. 또한 FGSM의 𝜀 크기에 따른 성능 변화도 함께 확인합니다.

초기 학습 샘플 비교
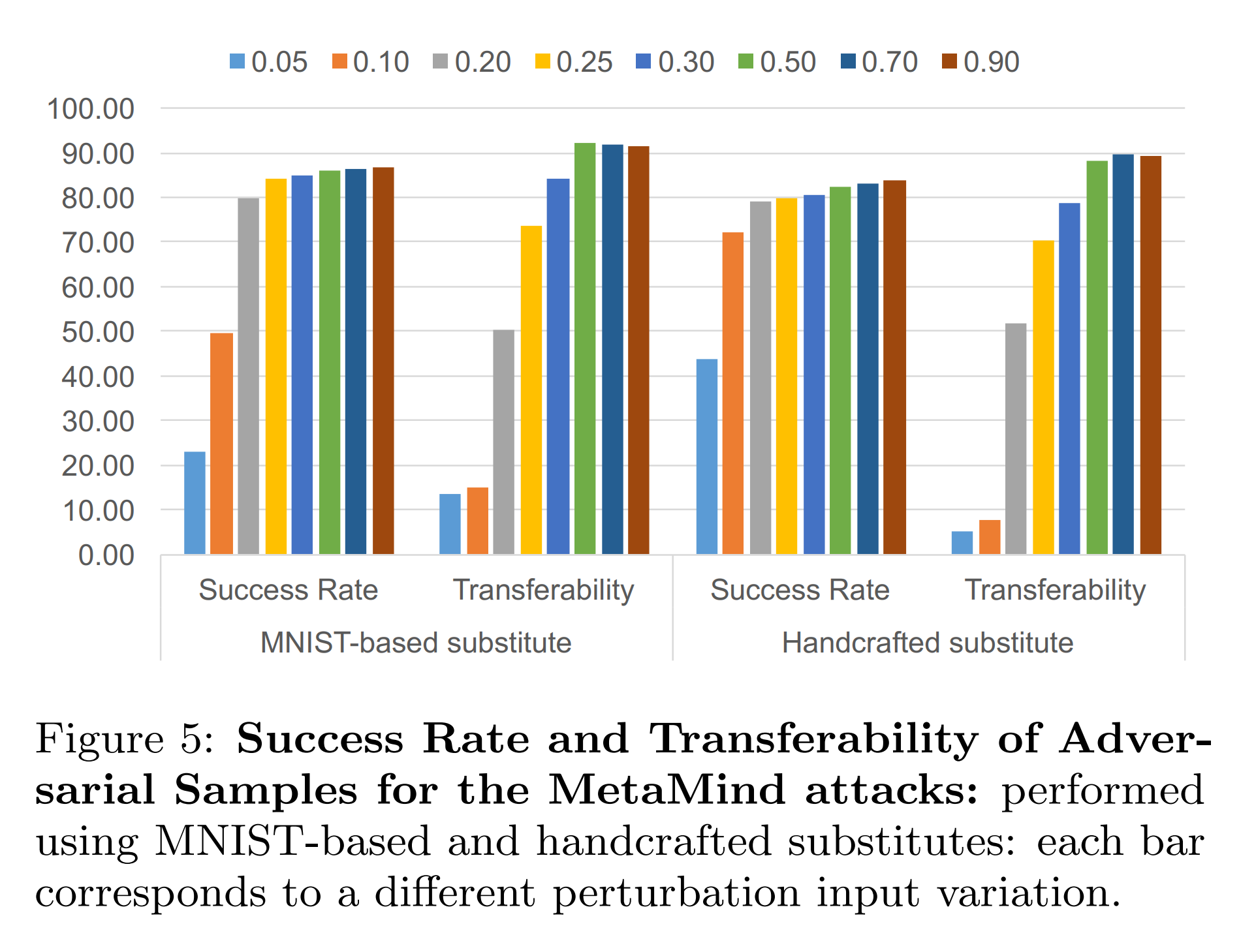
  • Success Rate: 적대적 예제가 대체 모델에서 오분류된 비율
  • Transferability: 동일한 적대적 예제가 원본 모델에서 오분류된 비율

위 결과를 보면, 두 대체 모델이 유사한 전이도를 보였습니다. 따라서 공격자가 오라클 학습 데이터에 접근할 수 없더라도 공격이 가능함을 시사합니다.

또한 아래 실험 결과는 대체 모델로 제작한 적대적 예제를 원본 모델에 입력한 결과를 보여줍니다. 대각 요소들은 원본 모델이 올바르게 분류한 경우, 비대각 요소들은 오분류한 경우입니다. 그 결과, 𝜀이 커질수록 원본 모델이 오분류하는 클래스가 일관되게 수렴하는 경향을 확인할 수 있습니다.

예측 결과와 정답 비교

보정 실험

목표

DNN 대체 모델 학습 과정, 적대적 예제 제작 과정에서 어떤 파라미터를 조정하면 대체 모델의 성능이 개선되는지 확인합니다.

대체 모델 학습 특징

  • 대체 모델 구조 대체 모델의 층 수, 크기, 활성함수, 유형과 같은 모델 구조의 선택은 전이도에 큰 영향을 미치지 않았습니다.

  • 에포크 수 대체 모델의 정확도가 포화 상태에 이르면, 이후 에포크를 늘려도 전이도가 개선되지 않았습니다.

  • 스텝 사이즈 λ 대체 모델 학습용 합성 샘플을 제작할 때 사용한 λ를 조정한 결과, 기준값 0.1에서 대체 모델의 정확도 변화가 ±3% 이내로 미미했습니다. λ를 키우면 수렴 안정성이 떨어졌고, λ를 줄이면 수렴 속도가 느려졌습니다.

    또한 아래 결과처럼 λ가 증가할수록 대체 모델의 전이도는 감소했습니다.

      λ = 0.1 λ = 0.3
    𝜀 = 0.25 22.35% 10.82%
    𝜀 = 0.5 85.22% 82.07%

대체 모델 학습 개선

  • PSS 합성 샘플은 아래 수식에 따라 매 라운드마다 추가됩니다.

    \[S_{\rho+1}=\{\;\vec{x}+\lambda_{\rho+1}\cdot \operatorname{sgn}\!\big(J_{F}[\tilde{O}(\vec{x})]\big)\;:\;\vec{x}\in S_{\rho}\;\}\cup S_{\rho}\]

    반복되는 재학습 과정에서 합성 샘플이 동일한 부호 방향으로 계속 변형되면, 결국 입력 범위([0,1])를 벗어나게 됩니다. 이를 해결하기 위해 입력을 유효 범위로 잘라내는 Clipping 작업이 필요하지만, 이 작업이 반복되면 합성 샘플들이 특정 영역에 집중되는 문제가 발생합니다. 그 결과, 대체 모델은 원본 모델의 결정 경계 주변을 정밀하게 탐색하기 어려워집니다.

    이를 해결하기 위해 본 논문은 PSS(Periodic Step Size) 방식을 사용합니다. PSS는 아래 수식처럼 스텝 부호를 주기적으로 뒤집어서 입력이 유효 범위에서 벗어나는 상황을 방지합니다.

    \[\lambda_{\rho}=\lambda\cdot(-1)^{\left\lfloor \rho/\tau \right\rfloor}\]

  • RS 대체 모델은 레이블 획득을 위해 오라클에 질의해야 합니다. 그리고 오라클 질의 수를 줄이는 것은 대체 모델 학습 비용 절감에 중요한 요소입니다. 기존 방식의 오라클 질의 수는 \(n\cdot 2^{\rho}\) 으로 매 라운드마다 두 배씩 증가했습니다.

    이를 개선하기 위해 본 논문은 RS(Reservoir Sampling)를 사용합니다. RS는 초기 σ 라운드까지는 기존 방식을 사용하다가, 이후 라운드부터는 \(S_{\rho+1}\) 에서 무작위 \(\kappa\) 개만 추출하여 학습에 사용합니다.

    \[n\cdot 2^{\sigma}+\kappa(\rho-\sigma)\]

    RS 방식을 사용하면 오라클 질의 수가 선형적으로 증가하지만, 대체 모델의 정확도는 약간 감소합니다. PSS와 함께 사용하면 정확도 감소를 줄일 수 있습니다.

적대적 예제 생성 특징

본 실험은 아래 표의 DNN 모델들을 대상으로 수행되며, 적대적 예제 생성 기법의 파라미터를 조정하며 대체 모델의 성능을 확인합니다.

실험용 DNN 모델들

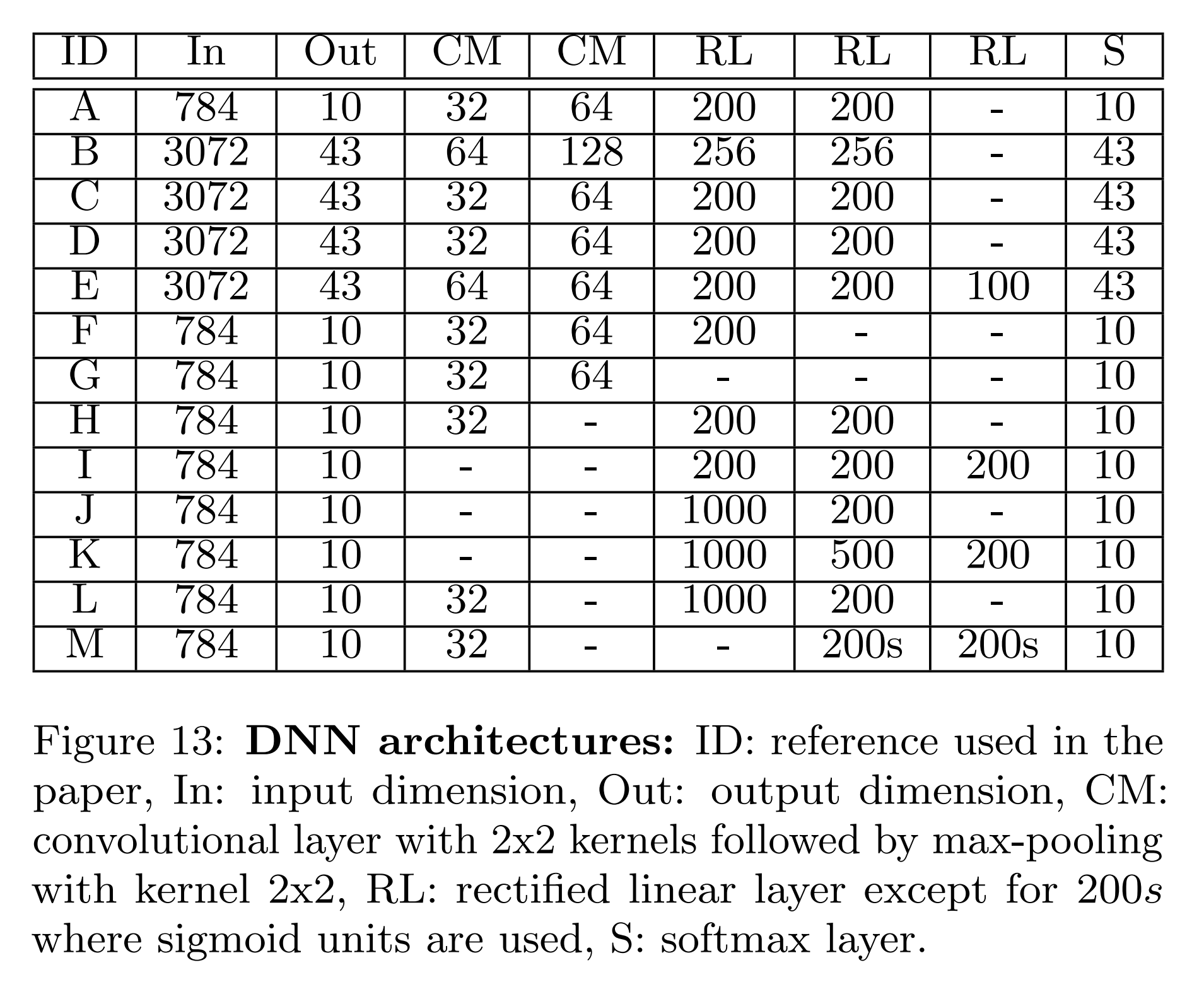
  • FGSM FGSM은 입력 데이터를 한 번에 변형하는 기법으로, 조정 가능한 파라미터는 𝜀 하나뿐입니다. 아래 실험 결과에 따르면, 모델 구조를 변경하더라도 𝜀 증가에 따른 전이도 증가 양상은 비슷했습니다. 그러나 𝜀를 증가시킬수록 사람 눈으로 구분 가능해지기 때문에 이 방식은 한계가 있습니다.

  </div>

</div>

𝜀 에 따른 FGSM 성능
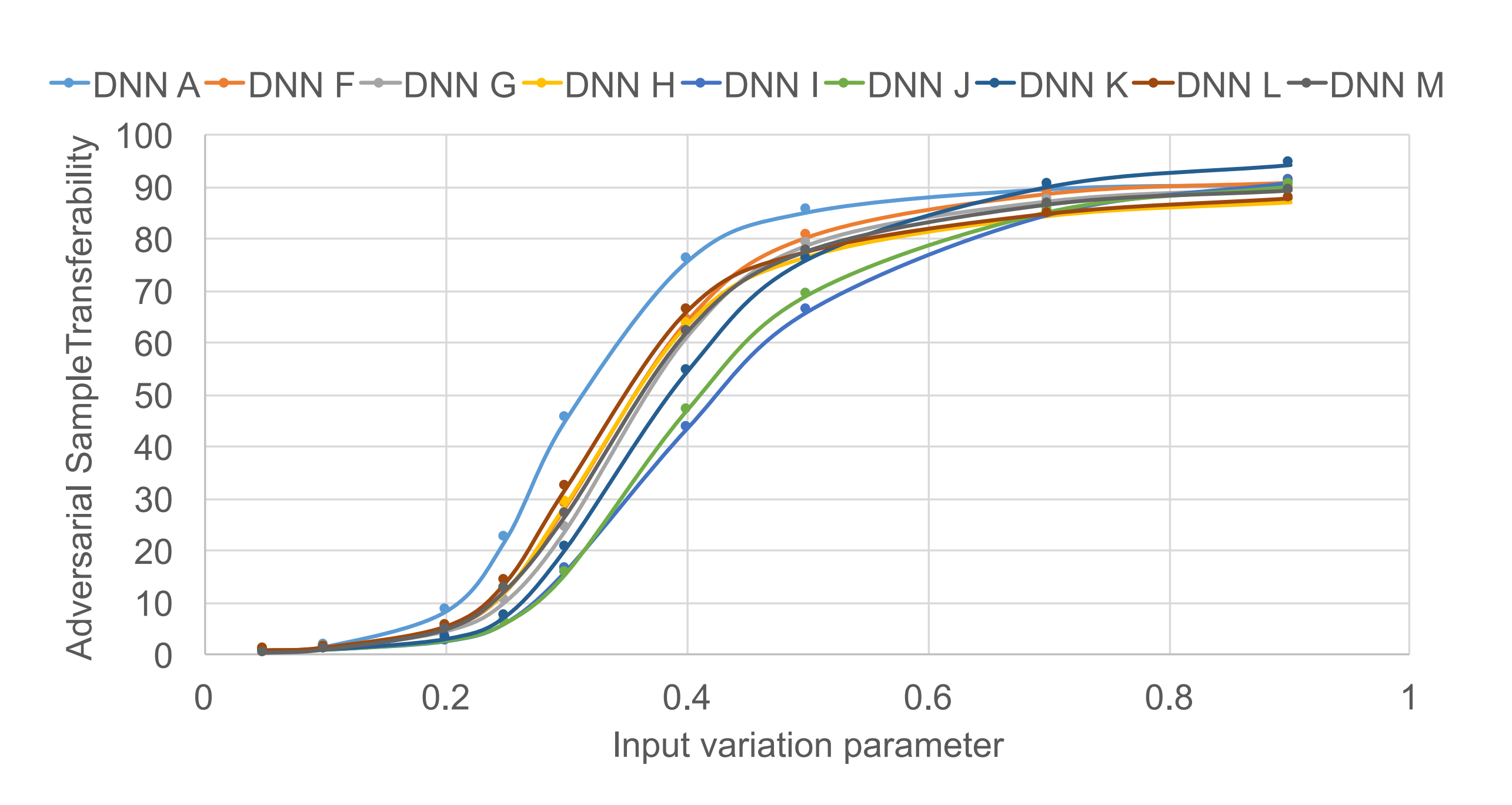
  • Papernot 알고리즘 최대 왜곡 \(\Upsilon\) 은 Saliency value를 바탕으로 결정되는 입력 데이터의 성분 중 변형할 비율입니다. 그리고 𝜀은 선택된 각 성분에 더할 변형의 크기입니다. 이 두 파라미터를 조정하여 Papernot 알고리즘의 성능을 개선할 수 있습니다.

적대적 예제 생성 비교

FGSM과 Papernot 알고리즘은 적대적 예제 생성 방식이 다릅니다. FGSM은 모든 입력 성분을 한 번에 조금씩 바꾸고, Papernot 알고리즘은 일부 입력 성분만 크게 변형합니다. 본 실험은 동일한 총 변형량에서 두 방식의 전이도 차이를 확인합니다. 이를 위해 아래 수식대로 총 변형량의 L1-norm을 고정하고 실험을 진행합니다.

\[\|\delta \mathbf{x}\|_{1}=\varepsilon\,\|\delta \mathbf{x}\|_{0}\]
  FGSM Papernot
\(∥δ \mathbf{x} ∥_1\) 총 변형량 총 변형량
\(𝜀​\) \(𝜀\) \(𝜀\)
\(∥δ \mathbf{x} ∥_0​\) \(1\) \(\Upsilon\)
$$\Upsilon$$ 에 따른 Papernot 알고리즘 성능

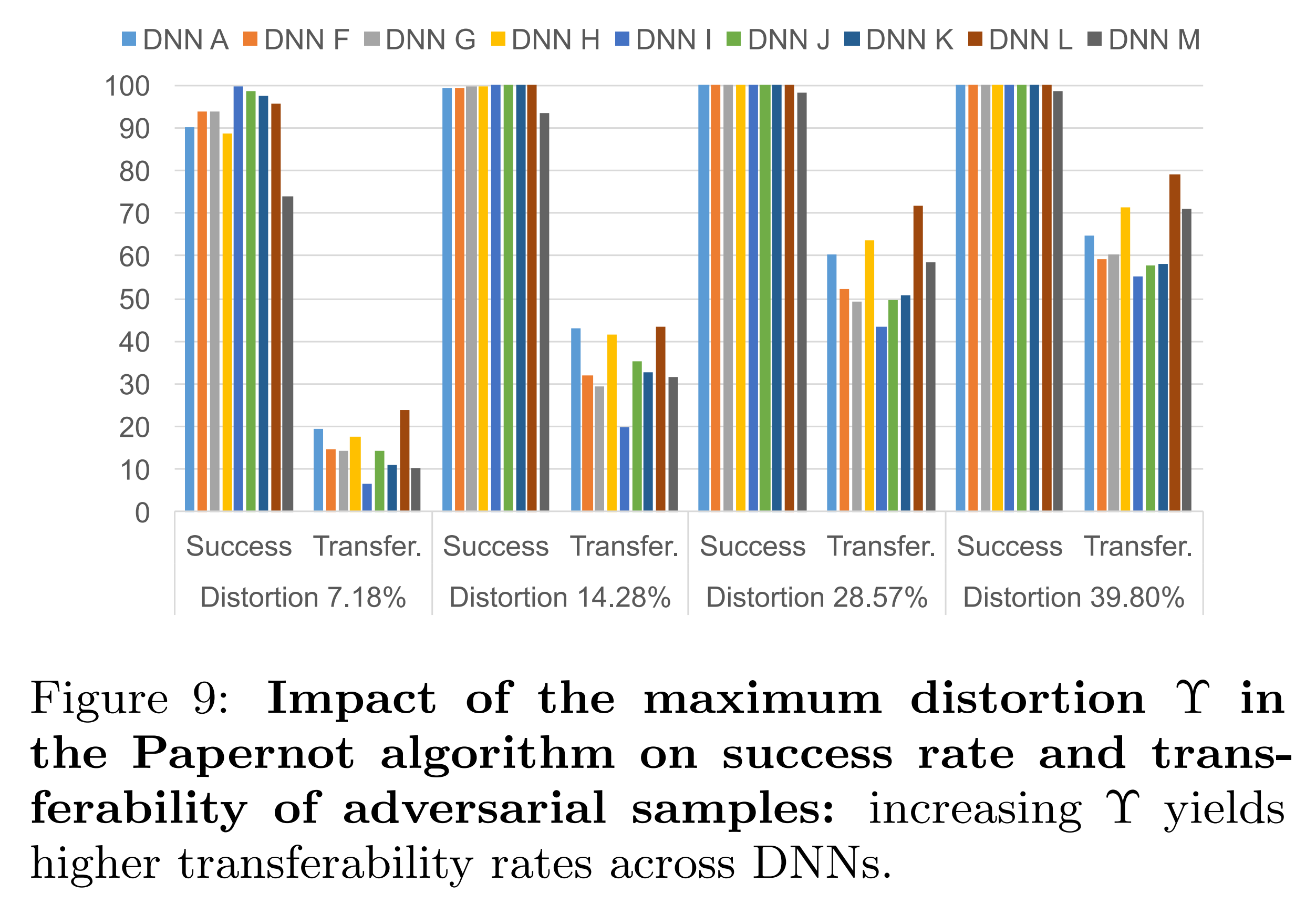
위 실험 결과는 𝜀의 크기를 1로 고정한 상태에서 \(\Upsilon\) 만 조정한 결과입니다. \(\Upsilon\) 이 클수록 대체 모델의 전이도가 증가하는 모습을 보입니다.

𝜀 에 따른 Papernot 알고리즘 성능

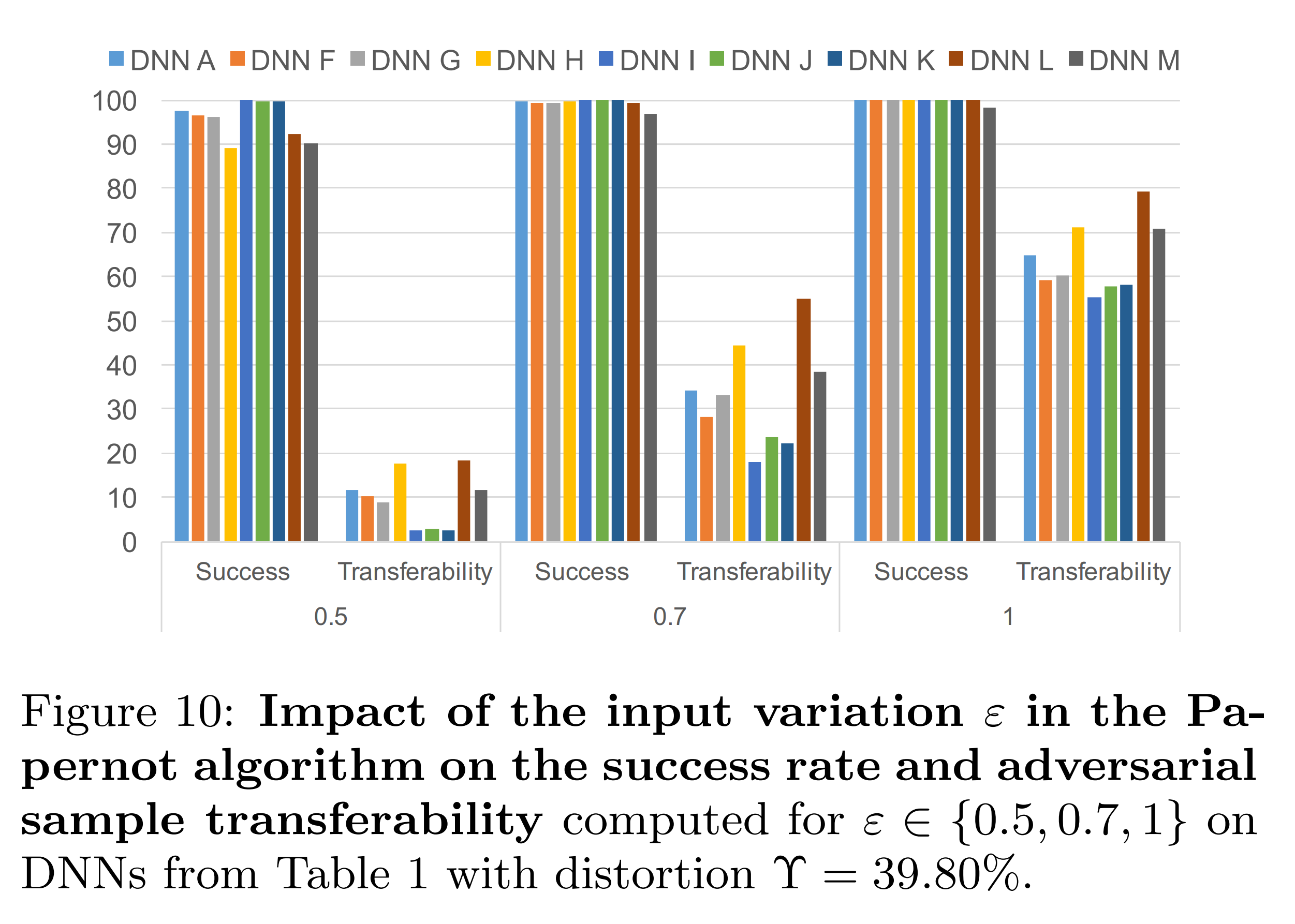
위 실험 결과는 \(\Upsilon\) 의 크기를 39.80%로 고정한 상태에서 𝜀만 조정한 결과입니다. 𝜀이 작을수록 대체 모델의 전이도가 감소하는 모습을 보입니다. 이는 \(\Upsilon\) 이 고정된 탓에, 작아진 변형 크기를 보상할 수 없었기 때문입니다.

따라서 본 논문은 원하는 변형 방식에 따라 적대적 예제 생성 알고리즘 선택이 달라진다고 결론짓습니다.

  • FGSM: 입력의 모든 성분을 조금씩 변형. 𝜀 조절 특화
  • Papernot 알고리즘: 입력의 일부 성분만 크게 변형. \(\Upsilon\) 조절 특화

일반화 실험

실험 환경

지금까지 실험한 대체 모델과 오라클은 모두 DNN 모델이었습니다. 하지만 이번 실험에서는 일반화 가능성을 평가하기 위해 다양한 환경에서 실험을 진행합니다. 이에 따라 본 실험은 대체 모델로 DNN과 LR을, 오라클로 DNN, LR, SVM, DT, kNN, 클라우드 원격 모델을 사용합니다.

대체 모델의 초기 학습 데이터는 MNIST의 테스트셋이며, PSS와 RS 기법도 적용합니다.

대체 모델 학습 일반화 성능

대체 모델이 미분 가능하다면, 오라클이 DT처럼 미분 불가능하더라도 학습이 가능합니다. 이때 대체 모델이 미분 가능해야 하는 이유는 Jacobian 기반으로 합성 샘플을 생성해야 하기 때문입니다.

LR은 소프트맥스 확률 벡터를 출력하기 때문에 DNN과 동일한 방식으로 Jacobian을 계산할 수 있고, 대체 모델로 사용될 수 있습니다.

대체 모델과 오라클의 예측 일치

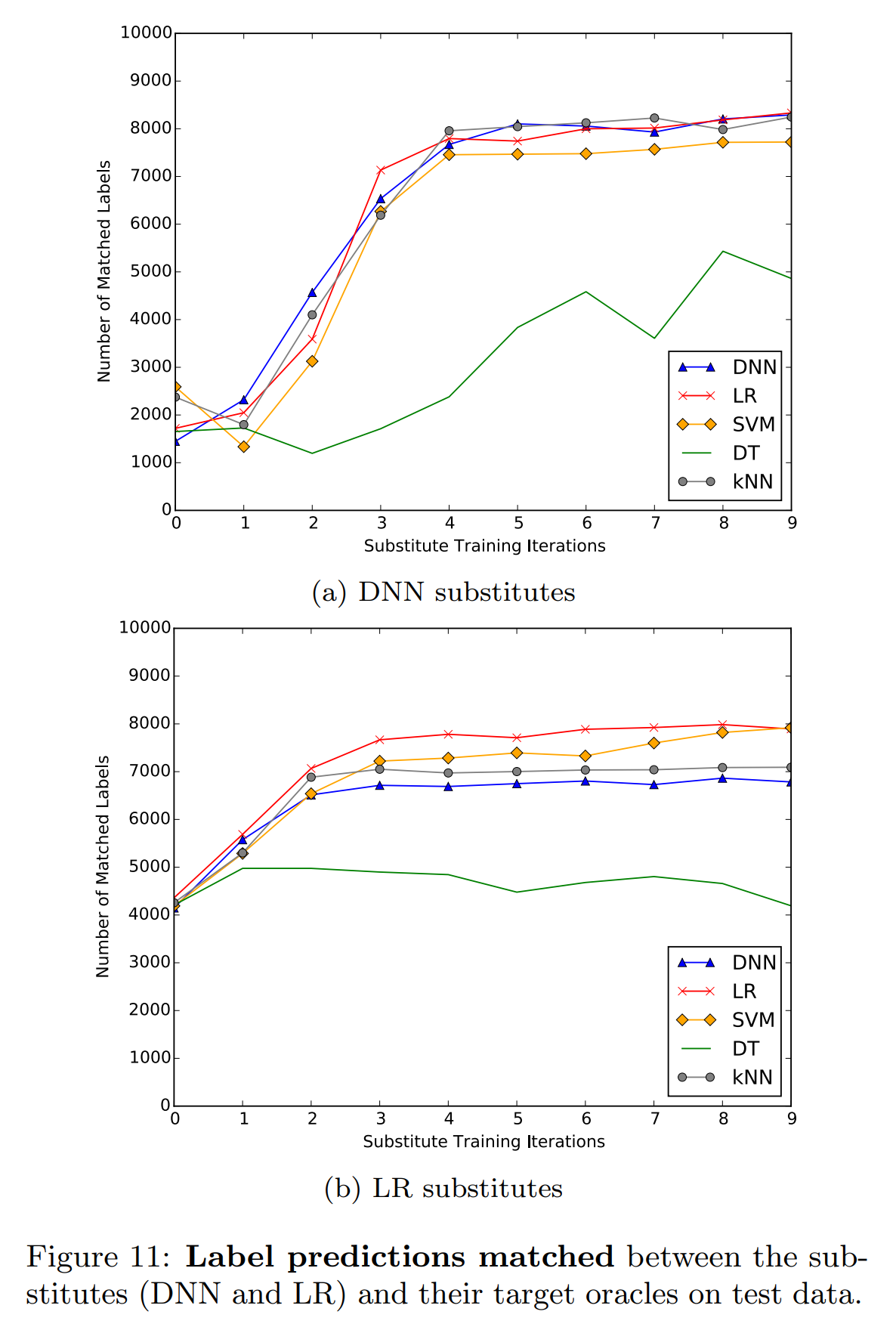
위 두 실험 결과를 보면, LR 대체 모델의 성능이 전반적으로 DNN 대체 모델보다 낮은 모습을 보여줍니다. 그러나 오라클이 LR, SVM일 때는 LR 대체 모델이 더 우세합니다. 특히 LR 대체 모델은 더 이른 라운드에서 수렴하는 경향을 보입니다.

PSS, RS 성능

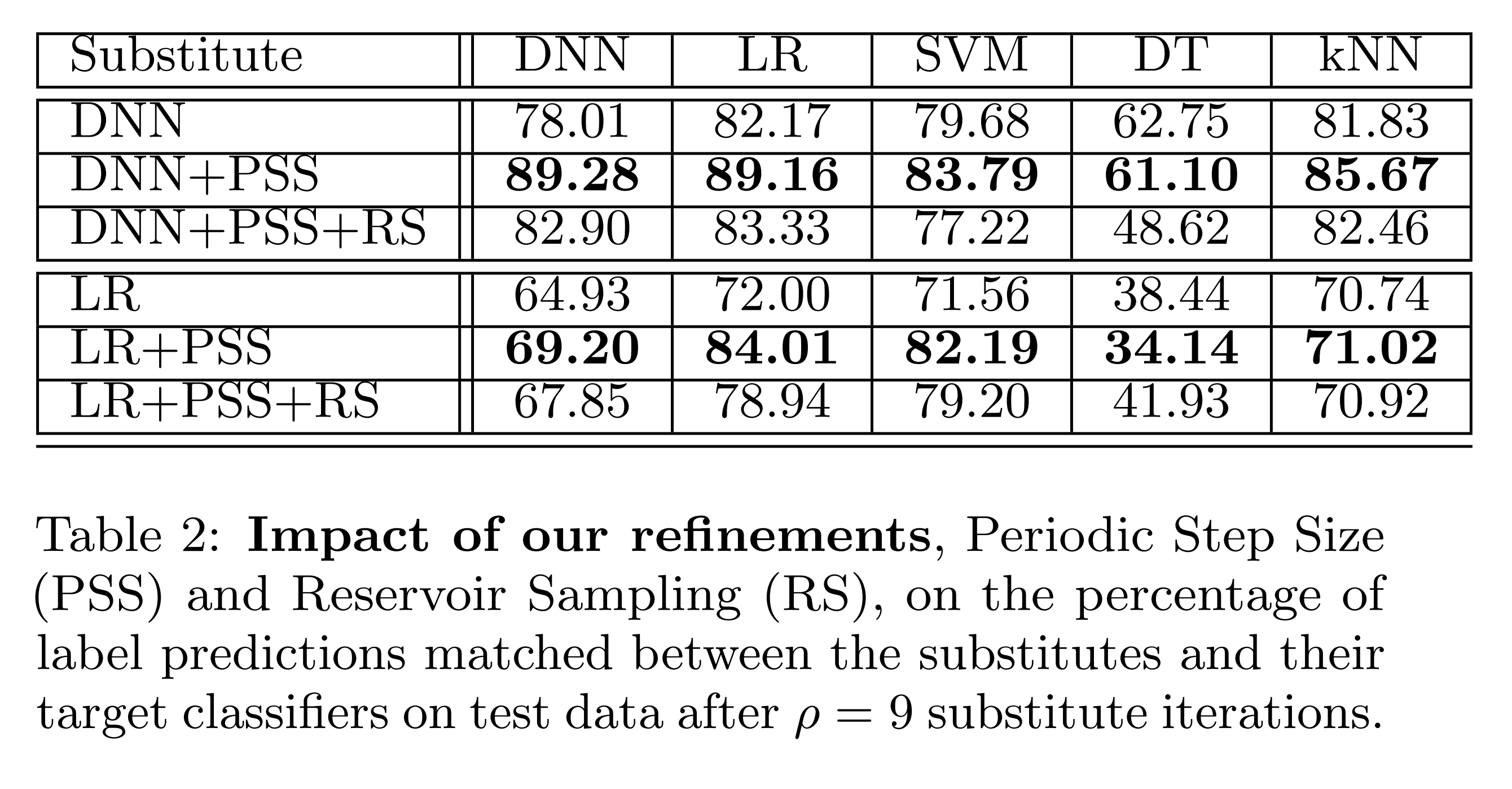
위 결과를 보면, PSS를 사용할 때 대체 모델과 오라클의 예측 일치율이 크게 개선됩니다. 그리고 RS를 PSS와 함께 사용하면, 바닐라 방식보다 우수한 모습을 보입니다.

오라클의 적대적 예제 오분류율

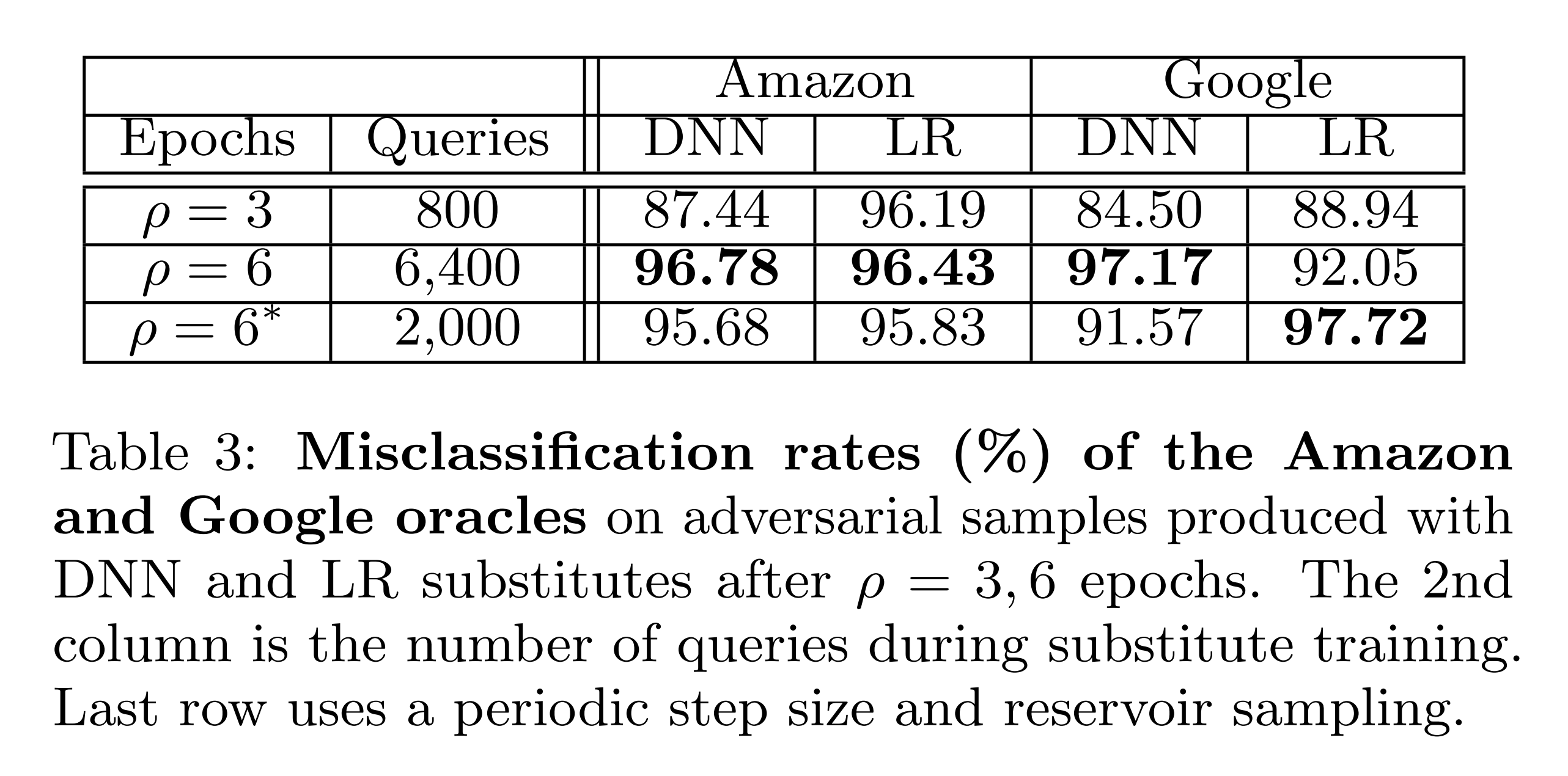
위 실험은 대체 모델에서 FGSM 방식으로 MNIST 테스트셋 10,000장에 대한 적대적 예제를 생성하고, 이를 오라클에 입력했을 때의 오분류율입니다.

오라클로 Amazon, Google의 원격 모델을 사용합니다. 그 결과, 전반적으로 높은 오분류율을 확인할 수 있습니다. 또한 PSS와 RS를 사용하여 오라클 질의 수를 6,400회에서 2,000회로 줄였음에도 불구하고, 오분류율이 비슷하거나 오히려 높아진 모습도 보입니다.

방어 실험

배경

방어자는 이러한 공격들로부터 모델 성능을 방어하기 위해 다양한 방어 전략을 사용합니다. 적대적 예제 방어는 공격 탐지에 초점을 둔 반응형, 오라클을 자체를 더 견고하게 만드는 선제형으로 나뉩니다. 본 논문의 공격기법은 오라클 질의를 여러 공격자에게 분산시킬 수 있기 때문에, 방어자가 공격을 탐지하기 어렵습니다. 따라서 본 방어 실험은 오라클을 견고하게 만드는 방어 기법을 소개하고, 이에 대한 공격기법의 공격 성능을 확인합니다.

그래디언트 마스킹

많은 방어 기법들이 그래디언트 마스킹(Gradient Masking) 범주에 속합니다. 그래디언트 마스킹은 공격자가 오라클의 유용한 그래디언트를 획득하지 못 하도록 오라클을 변형하는 기법입니다. 이는 공격자가 오라클에 대한 직접적인 적대적 예제를 생성하기 어렵게 만듭니다.

하지만 공격자는 오라클의 그래디언트를 모르더라도, 해당 오라클의 평활화(Smoothing)된 버전이나 대체 모델로 적대적 예제를 생성하여 그래디언트 마스킹을 우회할 수 있습니다. 완벽한 방어 기법은 없으며, 본 논문에서도 실증적 효과가 입증된 적대적 학습, 방어적 증류를 분석합니다.

적대적 학습

적대적 학습(Adversarial Training)은 학습 과정 전반에 적대적 예제를 삽입하여 모델의 견고성을 높이는 기법입니다. 본 실험은 MNIST 데이터에 대하여 오라클을 적대적 학습시키고 공격 성공률을 확인합니다. 이를 위해 매 배치마다 FGSM으로 적대적 예제를 생성하고, 이를 바로 훈련 데이터에 포함한 뒤 다음 배치를 학습했습니다.

적대적 예제의 오분류 성공률

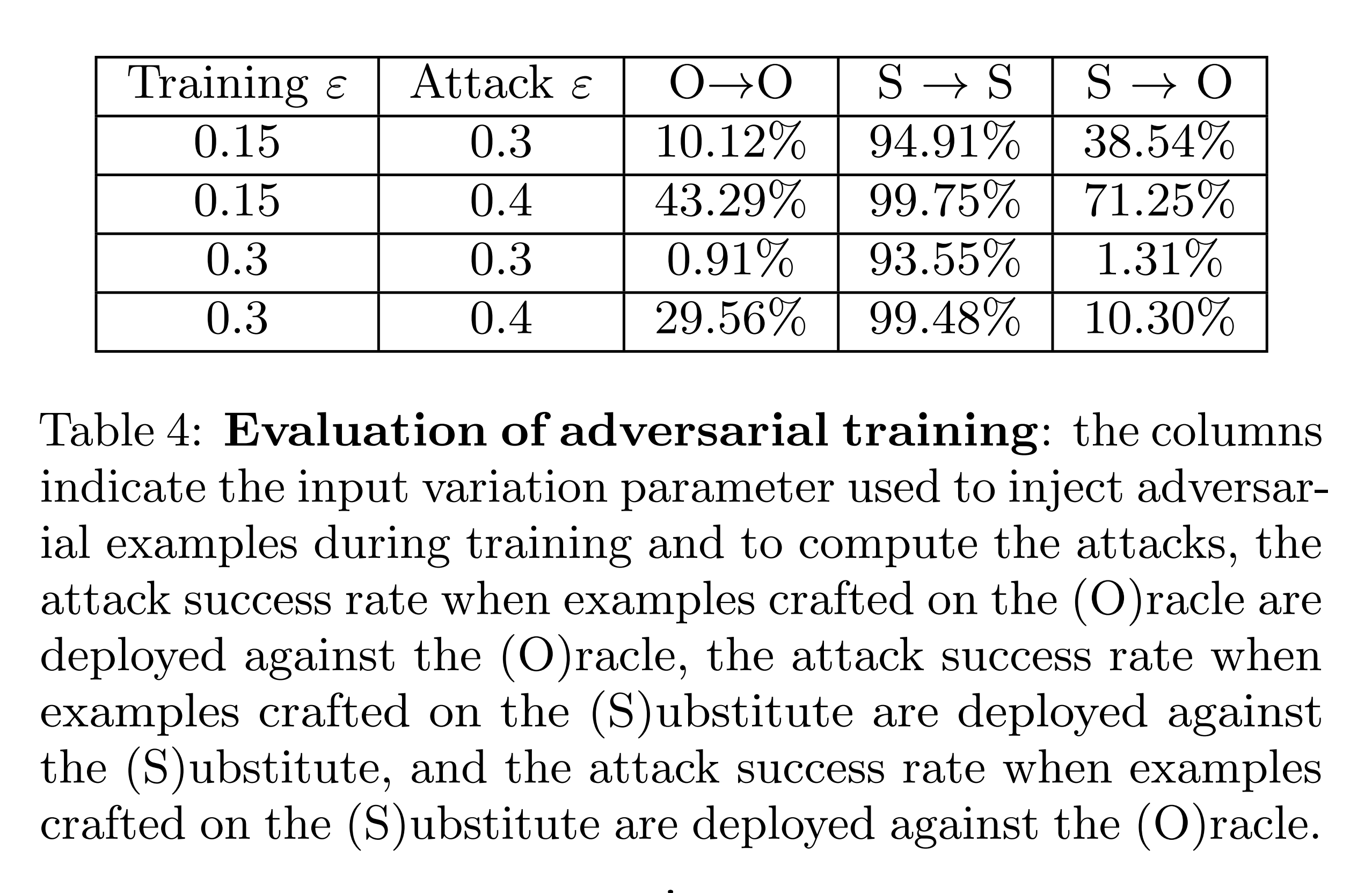
위 실험 결과를 보면, \(𝜀=0.15\) 에서 대체 모델로 생성한 적대적 예제가 오라클을 최대 71.25%까지 속입니다. 이는 작은 교란(\(𝜀=0.15\))에 대한 적대적 학습이 그래디언트 마스킹의 일종으로 작용하며, 대체 모델 기반 블랙 박스 공격에 취약함을 보여줍니다.

반면, 방어자가 \(𝜀=0.3\) 처럼 더 큰 교란까지 적대적 학습한다면, 해당 블랙 박스 공격에 견고한 모습을 보여줍니다.

방어적 증류

방어적 증류(Defensive Distillation)는 오라클을 증류해 공격자에게 유용한 그래디언트를 유출하지 않으려는 그래디언트 마스킹 기법입니다. 본 실험은 MNIST 데이터로 학습한 오라클을 증류한 뒤, 이에 대한 화이트 박스 공격과 블랙 박스 공격의 성공률을 비교합니다.

화이트 박스 공격: 증류된 오라클에서 직접 FGSM으로 적대적 예제를 생성하고, 이를 증류된 오라클에 입력합니다.

블랙 박스 공격: 증류된 오라클로 만든 대체 모델에서 FGSM으로 적대적 예제를 생성하고, 이를 증류된 오라클에 입력합니다.

방어적 증류 성능

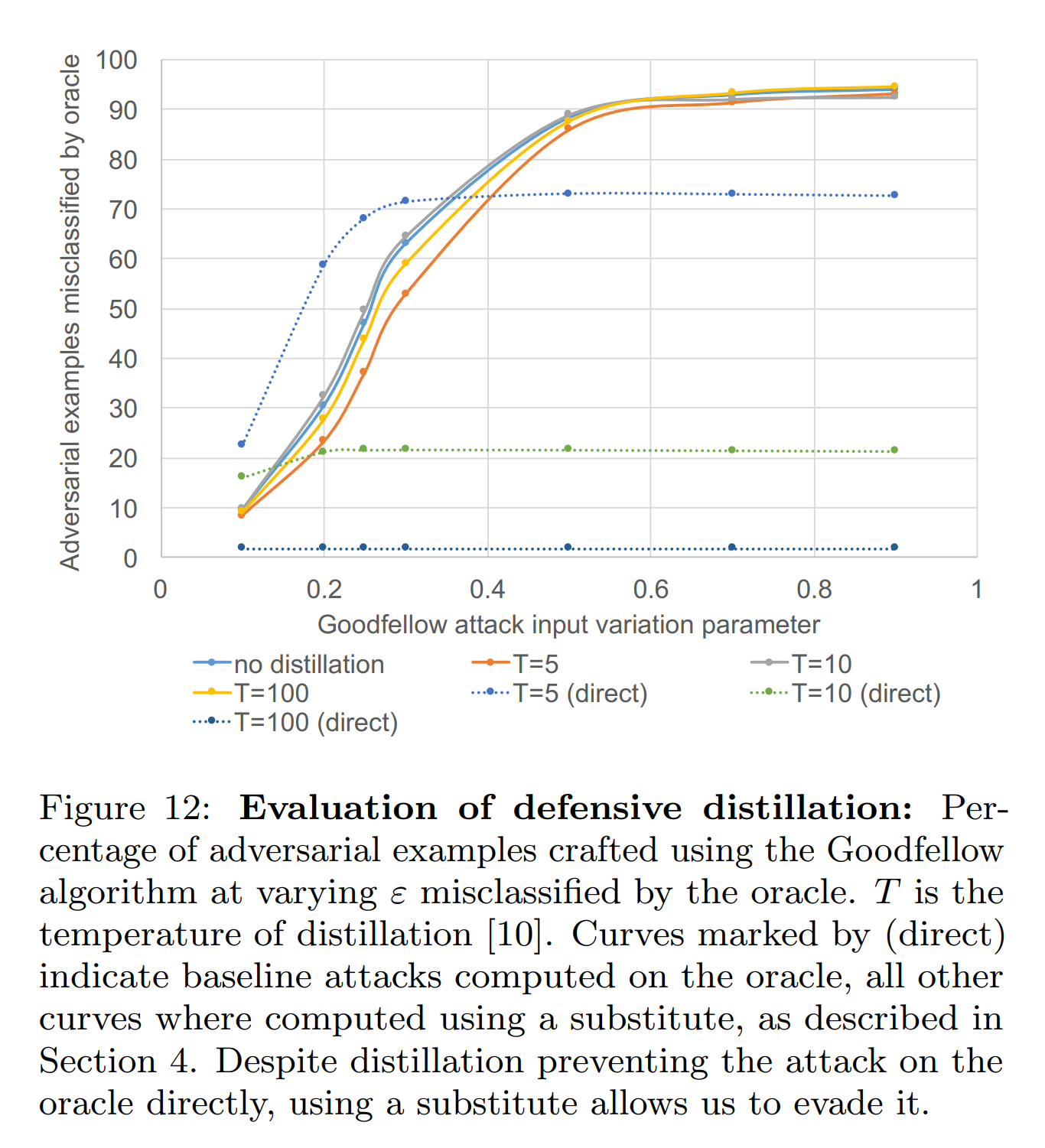
위 그래프를 보면, 방어적 증류는 화이트 박스 공격(direct)에 대하여 효과적인 방어 성능을 보입니다. 이는 증류 과정에서 학습 데이터 주변에서 오라클의 그래디언트가 감소하기 때문에, 증류된 오라클에 대한 FGSM의 성능이 낮아지기 때문입니다.

반면, 블랙 박스 공격에 대해서는 오라클의 증류 온도 \(T\) 와 무관하게 낮은 방어 성능을 보입니다. 이는 대체 모델이 증류된 오라클로부터 그래디언트가 아니라 오직 레이블만 가져오는 탓에, 대체 모델의 그래디언트는 감소하지 않았기 때문입니다. 그 결괴, 대체 모델은 FGSM 공격에 필요한 충분한 그래디언트를 유지하고, 그 결과 블랙 박스 공격의 성능이 높게 나타납니다.

  그래디언트 마스킹 적대적 학습 방어적 증류
화이트 박스 공격 어느 정도 견고 견고 견고
블랙 박스 공격 취약 큰 교란까지 학습해야 견고 취약

결론

본 연구는 모델의 내부 구조나 학습 데이터에 대한 정보 없이 오라클에 레이블만 질의할 수 있는 블랙박스 환경을 전제로 합니다. 이를 기반으로 합성 샘플을 활용해 대체 모델을 학습시켜 오라클을 속이는 공격 기법을 제안했습니다.

공격자는 오라클 질의를 통해 얻은 레이블을 이용해 Jacobian 기반 증강을 반복하며 대체 모델의 결정 경계를 오라클에 가깝게 근사시킵니다. 이후 대체 모델로 생성한 적대적 예제를 오라클에 전이시켰습니다. 그 결과, 원격 DNN에서 84.24%, Amazon과 Google 오라클에서 각각 96.19%와 88.94%의 오분류율을 달성했습니다. 게다가 그래디언트 마스킹 기반 방어를 무력화하는 뛰어난 성능을 보여줍니다.

이러한 성과는 블랙박스 공격의 실용성을 높이는 데 기여할 수 있습니다.