논문명: TOWARDS REVERSE-ENGINEERING BLACK-BOX NEURAL NETWORKS
저자: Seong Joon Oh, M. Augustin, M. Fritz, and B. Schiele
게재지: International Conference on Learning Representations (ICLR), Vancouver, B.C., Canada, 2018
서론
블랙박스 모델(Black-box model)이란, 오직 입력에 대한 출력만 관찰할 수 있고 내부 동작이나 구조에 대한 정보등의 내부 속성(Attribute)은 알 수 없는 모델을 말합니다. 화이트박스 모델은(White-box model)은 반대로 내부 속성이 모두 알려진 모델을 말합니다.
여기서 모델의 속성이란 모델의 종류, 네트워크의 깊이 및 연결 구조, 활성화 함수(Activation Function) 등을 포함한 모델의 아키텍처(Architecture), 학습 시 사용된 최적화 과정(Optimisation process), 그리고 훈련 데이터의 특성 및 분포 정보 등을 의미합니다.
많은 모델들은 지식 재산(Intellecutal Property) 보호나 훈련 데이터에 포함된 프라이버시(Privacy) 보호를 위해 블랙박스 모델 형태로 설계되어 배포됩니다.
하지만 이러한 내부 속성이 공개되지 않은 블랙 박스 모델은 역공학(Reverse Engineering) 기법을 통해 내부 속성을 추론당할 수 있습니다.
추론된 내부 속성은 더 정교한 적대적 공격 샘플(Adversairal Samples)을 생성하는데 사용되어 모델에 위협이 될 수 있습니다.
반대로, 얼굴 이미지처럼 개인정보 노출이 우려되는 콘텐츠에 대한 프라이버시 보호 목적의 적대적 샘플을 생성하는 데도 활용될 수 있습니다.
본 논문은 블랙박스 모델에 대한 역공학이 어떠한 방식으로 수행될 수 있는지에 대해 제안하며 실험을 통해 분석하고, 제안된 방법이 다양한 모델과 상황에서 일반화 가능성을 갖는지를 추가 실험을 통해 검증합니다.
본론
실험의 목표
본 논문에서의 실험은 어떠한 블랙박스 모델에 대해 입력 쿼리를 넣었을 때, 그 출력값을 이용해 모델의 내부 속성을 추론하는 것을 목표로 합니다.
Meta Training Set & Metamodel
특정 블랙박스 모델을 추론하기 위해서 먼저 그 블랙박스과 일정 수준 이상 유사할 것으로 예상되는 다양한 화이트박스 모델들을 수집하여 데이터셋으로 구성합니다. 이를 메타 학습용 데이터셋(Meta-training Set)이라고 합니다.
이후 다양한 화이트박스 모델들의 출력값을 입력값으로 받아 해당 모델의 속성을 출력하는 또 다른 모델을 학습시킵니다. 이를 메타모델(Metamodel)이라고 합니다.
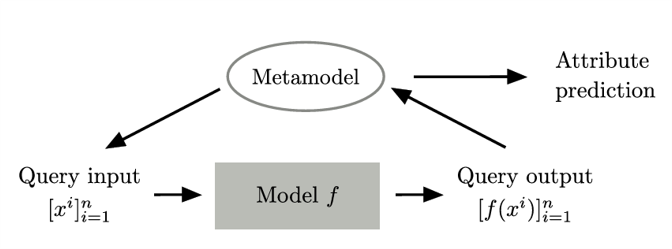
본 논문에서 최종적으로 제시하는 메타모델의 구조는 그림과 같습니다. 예측하고자 하는 블랙박스 모델에 대해 메타 모델이 n개의 이상적인 입력 쿼리를 생성한 후, 그 입력 쿼리가 블랙박스 모델을 거쳐서 나온 출력값을 다시 메타모델이 입력값으로 받아 최종적으로 모델의 속성들에 대한 예측을 출력값으로 내놓습니다.
메타모델의 종류는 KENNEN-O, KENNEN-I, KENNEN-IO 세 가지로 구분됩니다.
KENNEN-O
KENNEN-O는 N개의 고정된 입력값 쿼리에 대해 모델의 모든 속성을 한 번에 예측합니다. 입력값 쿼리들은 데이터셋에서 랜덤하게 추출하여 사용하며, 이 쿼리들은 변하지 않고 학습 단계와 평가 단계에서 모두 사용됩니다. 전체적인 모델의 학습 구조는 다음 그림과 같습니다.
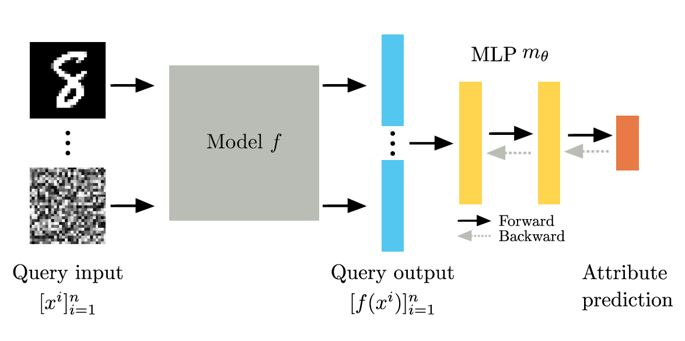
N개의 고정 쿼리를 메타 학습용 모델(화이트박스 모델)에 입력한 뒤, 그에 대한 출력값들을 순서에 민감하게(order-sensitive) 연결(concatenate)하여 분류기 m에 입력하고, 이를 통해 블랙박스 모델의 속성을 예측하도록 메타모델을 학습합니다.
이 학습 과정은 다음 수식으로 표현됩니다.
\[\min_{\theta} \ \mathbb{E}_{f \sim \mathbb{F}} \left[ \sum_{a=1}^{12} \mathcal{L} \left( m_\theta^a \left( \left[ f(x^i) \right]_{i=1}^{n} \right), y^a \right) \right]\]속성(Attribute)의 개수가 12개일 때, 각 메타 학습 데이터 샘플에 대해 모든 속성의 예측값과 실제 레이블 간의 Cross Entropy Loss를 합산하고, 전체 모델 분포에 대한 기대값을 최소화하는 방향으로 파라미터를 최적화합니다.
분류기는 은닉 유닛 1000개를 가진 두 개의 은닉층으로 구성된 MLP(multilayer perceptron)이며, 출력층은 12개의 속성 각각에 대한 병렬적인 선형 분류기(12-Linenar Classifers)로 구성됩니다.
분류기의 출력값은 각 속성에 대한 softmax값을 최종적으로 argmax하여 표현됩니다.
예시를 들어 설명해보겠습니다.
예측할 속성 총 3개는 다음과 같이 가정합니다.
- 속성 A: 클래스 3개
- 속성 B: 클래스 2개
- 속성 C: 클래스 4개
각 속성은 softmax를 통해 확률 분포로 예측됩니다.
| 속성 | 클래스 수 | Softmax 출력 |
|---|---|---|
| A | 3 | [0.1, 0.7, 0.2] |
| B | 2 | [0.6, 0.4] |
| C | 4 | [0.25, 0.1, 0.5, 0.15] |
이후 각 softmax 값은 argmax를 통해 하나의 정수값으로 표현되고, 각 속성에 대한 예측값이 최종 예측 결과로 출력됩니다.
# 각 속성별 softmax 출력에서 argmax 계산
[
argmax([0.1, 0.7, 0.2]) # → 1
argmax([0.6, 0.4]) # → 0
argmax([0.25, 0.1, 0.5, 0.15]) # → 2
]
# 최종 예측 결과
[1, 0, 2]
KENNEN-O는 신경망 기반 모델뿐 아니라 비신경망 기반 모델(non-neural networks)에도 적용이 가능합니다.
KENNEN-I
KENNEN-I는 KENNEN-O와 달리, 한 번에 하나의 입력 쿼리만을 입력값으로 받아 모델의 속성들을 한 번에 하나씩 개별적으로 예측할 수 있도록 학습합니다. Classifier m의 파라미터를 최적화하는 KENNEN-O와 달리, KENNEN-I는 개별적인 입력 쿼리를 최적화 하는 방식으로 학습이 이루어집니다.
KENNEN-I 모델의 구조는 다음 그림과 같습니다.
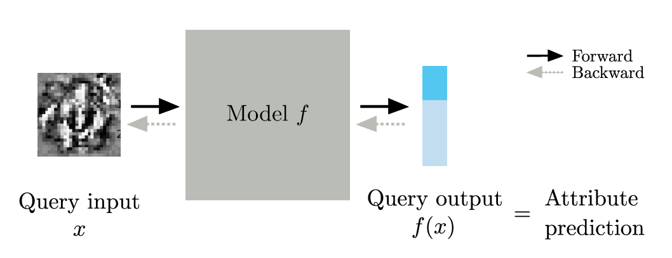
메타 학습 모델들의 출력값을 MLP 구조를 거쳐 모든 속성을 예측하도록 별도의 분류기 m을 학습하는 KENNEN-O와 달리, KENNEN-I는 어떠한 단일 입력 쿼리값을 메타 학습 모델에 넣었을 때, 메타 학습 모델의 출력값 자체가 자신이 설정한 속성의 예측값을 나타내도록 입력 쿼리를 최적화하도록 학습이 이루어집니다. KENNEN-O의 학습 목표를 수식으로 표현하면 다음과 같습니다.
\[\min_{x\colon \text{image}} \ \mathbb{E}_{f \sim \mathbb{F}} \left[ \mathcal{L} \left( f(x), y^a \right) \right]\]KENNEN-I의 작동 방식을 예시로 설명해 보겠습니다. 예측하고자 하는 블랙박스 모델이 MNIST 숫자 분류기(MNIST Digit Classifier)이며 KENNEN-I로 예측하고자 하는 속성이 모델의 합성곱 층(Conv layer)의 개수이고 예측하는 모델의 합성곱 층은 2개,3개, 또는 4개라고 가정 합니다. 모델의 합성곱 층의 개수 (2개,3개,4개)는 라벨로 각각 (0,1,2)로 표현됩니다.
일반적인 숫자 이미지 입력에 대한 MNIST 숫자 분류기의 10개 숫자에 대한 확률의 값인 softmax값으로 표현되며, 각각의 softmax값은 이미지가 해당 숫자의 이미지일 확률을 나타내며 최종적으로 argmax를 통해 가장 확률이 높은 숫자를 출력합니다.
| Model | f(x) | Argmax | Meaning |
|---|---|---|---|
| f | [0.89, 0.02, 0.02, …, 0.03] | 1 | Predicted digit = 1 |
반면 KENNEN-I를 통해 최적화된 입력 쿼리값이 블랙박스 모델 g에 들어가면, 출력값은 10개 숫자에 대한 확률의 값인 softmax로 동일하게 표현되지만, 각각의 softmax 값은 해당하는 학습 시 설정한 속성에 대한 확률값으로 표현됩니다.
예시에서는 합성곱 층의 개수 (2개,3개,4개)를 라벨 (0,1,2)로 매핑하였으므로, g(x)의 softmax를 argmax한 결과가 0이 나왔을 경우 그 의미는 입력 이미지가 숫자 0을 나타내는 이미지라고 예측하는 것이 아닌 블랙박스 모델의 합성곱 층의 개수가 2개라고 예측하는 것입니다.
| Model | Attribute | Ground Truth label | g(x) | Argmax | Meaning |
|---|---|---|---|---|---|
| g_1 | #Conv layer : 3 | 1 | [0.01, 0.89, 0.02, …, 0.03] | 1 | Model has 3 Conv layer |
| g_2 | #Conv layer : 2 | 0 | [0.87, 0.04, 0.02, …, 0.01] | 0 | Model has 2 Conv layer |
KENNEN-I는 단순한 입력-출력 쌍으로 속성의 추론이 가능하게 하는 점에서 유용하지만, 몇 가지의 한계도 가지고 있습니다.
첫째, 각 속성에 대해 모델을 개별적으로 학습해야 하므로, 모든 속성에 대한 예측을 한 번에 수행하기 어렵습니다.
둘째, 모델의 속성이 출력 차원을 초과하는 클래스 수를 가지는 경우 예측이 불가능합니다.
셋째, 모델을 통해 최적화된 입력값이 일반적인 입력과 달라, 탐지 회피성(stealth) 측면에서 취약할 수 있습니다.
이러한 한계를 보완하기 위해 KENNEN-I과 KENNEN-O를 결합한 방식인 KENNEN-IO 모델이 제안됩니다.
KENNEN-IO
KENNEN-IO는 n개의 입력 쿼리를 최적화하는 과정과, 분류기 m을 최적화하는 과정을 모두 포함합니다.
KENNEN-IO의 학습 목표를 수식으로 표현하면 다음과 같습니다.
\[\min_{\{x^i\}_{i=1}^{n} \, \text{: images}} \ \min_{\theta} \ \mathbb{E}_{f \sim \mathbb{F}} \left[ \sum_{a=1}^{12} \mathcal{L} \left( m_\theta^a \left( \left[ f(x^i) \right]_{i=1}^{n} \right),\ y^a \right) \right]\]위 수식은 n개의 입력 쿼리 메타 분류기 m을 Cross Entropy의 평균을 최소화하는 방향으로 동시에 학습한다는 의미입니다.
학습 방식은 먼저 학습 초기 200 epoch 동안은 KENNEN-O 방식으로 분류기 m을 먼저 학습합니다.
이후 후 추가적인 200 epoch 동안, n개의 입력 쿼리와 분류기의 파라미터를 50 epoch마다 번갈아가며 교대로 업데이트합니다.
KENNEN-IO는 KENNEN-I의 쿼리 최적화와 KENNEN-O의 모든 속성 동시 예측을 통합한 발전된 메타모델 구조입니다.
Experiment
실험 환경 설정
위 모델들을 실험하고 검증하기 위해, 본 논문에서는 블랙박스 모델과 메타 학습 모델(화이트박스 모델)은 MNIST 숫자 분류기(MNIST Digit Classifer)를 사용합니다. 모델의 속성은 총 12가지로, 각 속성별로 다양한 값을 사용하여 다양한 메타 학습 모델을 구성합니다.
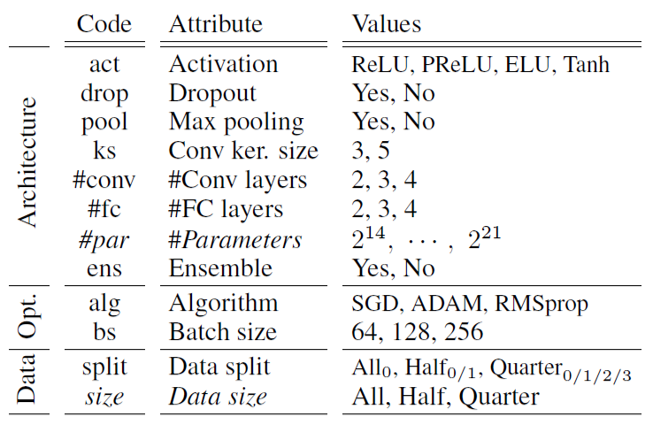
12개 속성들의 가능한 조합 수는 총 18,144개입니다. 여기에서 Random seed를 0~999까지 1000개로 설정하여 총 18,144,000개의 MNIST SET을 만들었습니다. 이 중 10,000개의 모델을 랜덤으로 선택하고 MNIST의 학습시켰습니다. 학습 결과 정확도가 98% 미만인 모델은 제거하고, 동일한 아키텍처를 기반으로 앙상블(Ensembles)을 구성하여 최종적으로 11,252개의 모델들을 확보했습니다.
추출한 모델들을 5,000개는 훈련 모델, 1,000개는 평가 모델, 그리고 나머지 5,252개의 모델로 나누었습니다.
이 때 모델들을 나누는 방법은 두 가지가 사용되었습니다.
첫 번째 방법은 Random Split입니다. 이 방법은 말 그대로 무작위로 모델들을 나누는 방법입니다.
두 번째 방법은 Extrapolation Split입니다. 이 방법은 메타모델이 훈련에 사용된 모델들과는 다른 종류의 블랙박스 모델에 대해서도 잘 작동하는지 평가하기 위해, 의도적으로 도메인 간 간극(domain gap)을 만들어 학습/평가 데이터를 분리하는 방식을 사용합니다.
예시:
#layers(합성곱 층의 수)를 기준으로,얕은 모델들 (예:
#layers < 10) → 메타 학습용(training set)깊은 모델들 (예:
#layers ≥ 10) → 테스트용(test set)
이처럼 속성을 기준으로 분할하면 모델이 훈련 시에 본 적이 없는 구조에 대한 예측도 할 수 있는지 일반화 성능을 측정할 수 있습니다.
학습 및 평가
먼저 Random(R) Split 방법으로 데이터를 분할한 후 학습 및 평가를 진행한 후에, 측정한 평가 지표를 살펴보겠습니다.
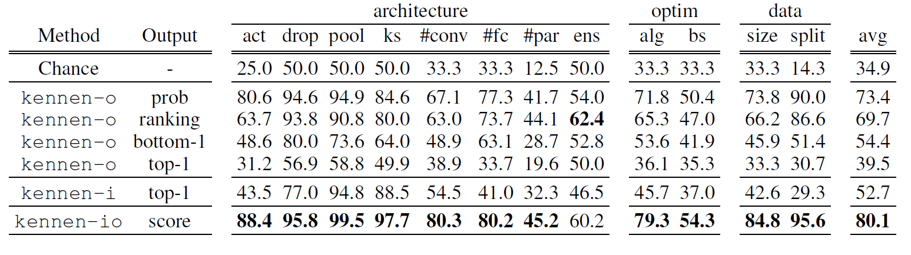
위 표의 Output은 모델이 메타 학습 모델의 출력값으로부터 사용한 값들을 의미하며 각각의 의미는 다음과 같습니다.
prob: softmax 확률 벡터 전체를 입력으로 사용 ranking: softmax 확률의 내림차순 클래스 순서를 사용 bottom-1: 확률이 가장 낮은 클래스만 사용 top-1: 확률이 가장 높은 클래스만 사용 score: softmax 확률 벡터 기반 요약치
평가 결과를 살펴보면, 모든 모델이 무작위 추측(Random Guess)보다 좋은 성능을 보이고 있는 것이 확인됩니다.
또한, bottom-1 output을 입력으로 사용한 KENNEN-O가 top-1 output을 입력으로 사용한 KENNEN-O보다 평균 예측률이 더 높은 것을 확인할 수 있습니다.
마지막으로, KENNEN-IO 모델이 다른 모델들보다 거의 모든 속성에 대한 예측을 더 잘 하고 있음을 볼 수 있습니다.
다음은 Extrapolation(E) Split 방법으로 데이터를 분할한 후 학습 및 평가를 진행한 후에, 측정한 평가 지표를 살펴보겠습니다.
이 분할 방법을 사용하면 일반적인 정확도가 아닌 다른 지표로 성능을 평가해야합니다. 그 이유는 일부 속성 클래스가 학습 데이터에 아예 존재하지 않고, 평가 데이터에만 존재할 수 있기 때문입니다. 따라서 이 경우, 분할 기준이 된 속성은 평가 대상에서 제외하고, 나머지 속성들에 대해서만 예측 정확도를 측정합니다.
예시 :
전체 속성 집합 A = {A1, A2, A3, A4}
분할 기준 속성 A’ = {A1}
E split Accuracy 측정에 사용되는 속성 : A \ A’ = {A2, A3, A4}
E-Split Accuracy를 측정한 후에, 이 방법이 Random Split에 비해 얼마나 성능이 좋은지 평가하기 위해 정규화된 정확도(Normalised Accuracy)를 측정합니다. 수식과 평가 결과는 다음과 같습니다.
\[\text{N.Acc}(\tilde{A}) = \frac{\text{E.Acc}(\tilde{A}) - \text{Chance}(\tilde{A})} {\text{R.Acc}(\tilde{A}) - \text{Chance}(\tilde{A})} \times 100\%\]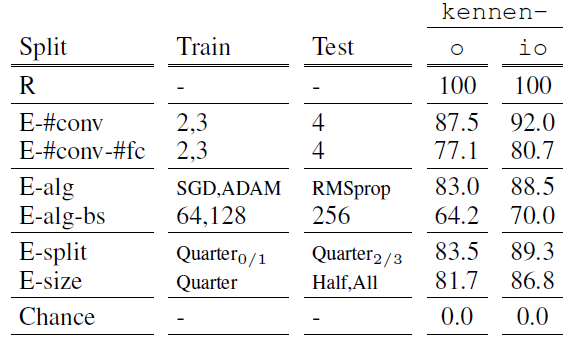
위 평가 지표는 E-Split에 사용한 속성과 모델에 따른 정규화된 정확도를 보여줍니다. 모두 N.Acc가 100% 이하로 E-Split Accuracy가 R-Split보다 낮지만, 모두 70% 이상의 성능을 보이며, E-split을 통해 블랙박스 모델이 메타 학습 모델과 도메인 간극이 있을 때에도 적용될 수 있도록 한 방법이 효과가 있음을 증명하였습니다.
또한, 실험한 모든 경우에서 KENNEN-IO가 KENNEN-O보다 약 5% 가량 더 좋은 성능을 보였습니다.
추가 분석
정규화된 정확도 외에, 이 정확도가 의미있는 결과인지 재검증하기 위해 Confusion Matrix를 분석해 보았습니다.
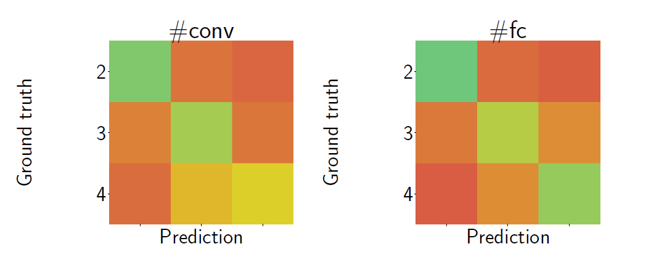
실제 값과 예측 값이 같은 값인 대각선 부분이 초록색으로 진할수록 더 잘 예측한 것을 의미하고, 그 외의 부분들은 빨간색이 진할수록 더 잘 예측한 것을 의미합니다. 그림을 살펴보면, 합성곱 층의 갯수가 인접한, 즉 2와 3인 모델들, 그리고 3과 4인 모델들에 대해서 2와4인 모델보다 서로 혼동한 부분이 더 옅은 빨간색으로 나타난다. 이것은 인접한 합성곱 층을 더 혼동한다는 것을 의미합니다.
이는 두 가지 시사점을 가집니다.
첫째로 , 신경망 출력 안에 의미적 속성 정보(레이어 수, 파라미터 수, 배치 크기 등)가 실제로 존재한다는 점입니다.
둘째로 , 메타모델이 단순히 아티팩트에 의존하는 것이 아니라 의미적 정보를 학습하여 일반화할 수 있다는 점입니다.
이처럼 정규화된 정확도와 더불어 혼동 행렬을 분석하므로써 본 실험이 의미있는 결과를 나타내고 있음을 증명하였습니다.
추가 실험
실험에서 사용된 MNIST 숫자 분류기와 더불어, 메타모델이 현실적인 이미지의 분류에도 적용될 수 있는지 증명하기 위해 ImageNet 분류기를 대상으로 추가적인 실험을 실시하였습니다.
이 실험에서 메타 모델은 KENNEN-O를 사용하였고, 학습/평가를 위해 사용하는 모델들은 5개의 서로 다른 모델 그룹(family)로 구성되어 있으며, 같은 그룹 내에서 서로 다른 버전을 포함해 총 19가지의 모델을 사용하였습니다.

성능을 평가할 속성은 모델 그룹으로 총 5개(S,V,B,D,R)의 클래스를 가집니다.
위의 모델들을 바탕으로 메타모델 KENNEN-O를 학습한 뒤, 모델 그룹에 대해 얼마나 잘 예측하는지 각 모델의 결과를 평균을 내어 정확도를 평가하였습니다.
모델의 성능을 신뢰성 있게 검증하기 위해 다음과 같은 방법으로 평가를 수행합니다.
-
교차 검증 (Cross Validation)
- 각 실험에서 모델 그룹(family)별로 무작위로 하나의 테스트 네트워크를 샘플링합니다.
- 이를 10회 반복하여 안정적인 평가 결과를 확보합니다.
-
ImageNet 검증 세트에서 쿼리 무작위 추출
- ImageNet 검증 데이터셋에서 쿼리를 무작위로 샘플링합니다.
- 각 실험마다 10개의 무작위 쿼리 집합을 선택합니다.
이렇게 총 100회의 쿼리 집합으로 평가를 수행한 결과, 정확도의 평균은 90.4%로 높은 정확도를 보였습니다.
쿼리 집합을 1000개로 늘려서 실험한 결과 정확도의 평균은 94.8%까지 상승했습니다.
이후 메타모델을 통한 모델 속성 예측이 모델을 적대적 이미지 교란(Adversarial Image Perturbations, AIPs) 공격에 얼마나 더 취약하게 만들 수 있는지를 추가 실험을 통해 확인하였습니다.
적대적 이미지 교란 공격에서 전이성(Transferability)이란, 한 모델에서 생성된 적대적 예제가 다른 모델에서도 성공적으로 오분류를 유발하는 능력을 의미합니다.
이번 추가 실험에서는 이 전이성 개념을 적용하여, 메타모델이 모델의 그룹(패밀리)을 예측할 수 있을 경우 모델이 더 취약해질 수 있다는 가정을 검증했습니다.
실험 결과, 같은 모델 계열(Within-family) 내에서 생성된 적대적 예제는 공격 성공률(오분류율)이 더 높게 나타났으며, 서로 다른 계열(Across-family) 간 전이성은 효과가 상대적으로 낮았습니다.
또한 적대적 이미지 교란 공격을 시행하였을 때 오뷴류율이 시나리오 별로 어떻게 다른지 확인하였습니다.

실험 결과를 보면, 화이트박스 모델은 오분류율이 100%였고, 모델의 그룹이 메타모델을 통해 예측된 블랙박스 모델의 오분류율은 모델의 그룹이 이미 알려져있던 블랙박스 모델의 오분류율과 비슷한 수치로 나타났습니다.
이는 메타모델이 모델의 계열을 정확히 예측할 수 있다는 점, 그리고 이것이 공격자에게 중요한 단서를 제공할 수 있으며 공격자가 이 정보를 활용해 보다 정교하고 효과적인 적대적 공격을 설계할 수 있음을 시사합니다.
결론
본 논문의 연구를 통해 제안된 메타모델은 입력-출력 쿼리 집합만으로도 블랙박스 모델의 다양한 속성을 효과적으로 예측할 수 있음을 보여주었습니다. 제안된 모델은 합성곱 층 수, 완전연결 층 수, 최적화 방식, 데이터 크기와 같은 모델의 구조적 특징을 별도의 내부 정보 없이도 추론하였습니다.
또한, 블랙박스 모델의 속성을 역공학으로 파악하면 해당 모델이 적대적 공격(Adversarial Attack)에 더 쉽게 노출될 수 있음을 전이성(Transferability)을 이용한 실험에서 같은 계열의 모델에 대해 공격 성공률이 현저히 높게 나타난 사실로 입증하였습니다.
이러한 결과는 메타모델이 모델의 속성을 예측할 수 있다는 사실이 공격자에게 중요한 단서를 제공할 수 있음을 의미합니다. 결국 공격자는 이 정보를 활용하여 보다 정교하고 효과적인 적대적 공격 샘플을 설계할 수 있게 됩니다.
따라서 블랙박스 모델을 설계하고 배포할 때는 성능뿐만 아니라 보안적 측면에서 속성 추론 공격에 대비할 수 있는 추가적인 방어 대책이 필요합니다.