논문명: EModel Stealing and Application
저자: Binghui Wang, Neil Zhenqiang Gong
게재지: Symposium on Security and Privacy SP, San Francisco, CA, 2018. IEEE.
서론
MLaaS (Machine Learning as a Service) 는 머신러닝 모델 개발, 학습, 배포, 관리를 클라우드 플랫폼(cloud platform)에서 제공하는 서비스입니다. MLaaS 덕분에 기업과 개인은 고성능 머신러닝 모델을 저비용으로 쉽게 활용할 수 있습니다. 그러나 MLaaS의 모델은 하이퍼파라미터 도용 (Hyperparameter Stealing) 위험에 노출될 수 있습니다.
하이퍼파라미터는 모델 성능을 결정하는 핵심 요소이며, 다양한 알고리즘에서 모델의 학습 방향을 조정합니다. 하이퍼파라미터를 학습하는 과정은 고비용을 수반하기 때문에 상업적 기밀로써 간주됩니다. 하지만 사용자가 학습 데이터와 모델 파라미터를 MLaaS와 공유하는 과정에서, 악의적 사용자가 하이퍼파라미터를 추출할 수 있습니다. 이는 MLaaS의 비용 구조를 우회하여 고성능 모델을 저비용으로 학습하려는 시도로 이어질 수 있습니다. 이러한 시도는 MLaaS의 상업적 가치를 저해할 수 있으므로 대응책이 필요합니다.
이러한 배경 속에서 본 논문은 하이퍼파라미터 도용 공격을 분석하고 방어 기법을 제안합니다. 또한 Amazon Machine Learning과 같은 실제 MLaaS 플랫폼에서 다양한 알고리즘을 대상으로 하이퍼파라미터 도용 공격을 실험하고, 그 효과를 입증합니다. 나아가 모델 파라미터를 반올림 (Rounding) 하는 방어 기법의 성능과 한계를 제시합니다.
사전지식
하이퍼파라미터 vs 모델 파라미터
하이퍼파라미터(Hyperparameter)는 머신러닝 모델의 학습 과정을 조정하는 변수로, 모델 성능에 직접적인 영향을 미칩니다. 아래 수식의 하이퍼파라미터 λ는 목적 함수 L(w)에서 손실 함수와 정규화 항의 균형을 조정하여 과적합을 방지합니다.
\[\begin{align} \mathcal{L}(\mathbf{w}) = \mathcal{L}_{\text{loss}}(\mathbf{w}) + \lambda \mathcal{R}(\mathbf{w}) \end{align}\]모델 파라미터(Model Parameter)는 목적 함수를 최소화하는 과정에서 실제로 학습한 파라미터를 의미합니다. 모델 파라미터의 표현방식은 목적 함수의 종류에 따라 달라집니다.
비커널 알고리즘 vs 커널 알고리즘
비커널 알고리즘(Non-Kernel Algorithm)은 가중치와 데이터의 선형결합을 사용하는 알고리즘입니다. 목적 함수가 비커널 알고리즘이면 모델 파라미터는 w로 표현됩니다. \(\begin{align} \mathcal{L}(\mathbf{w})=\mathcal{L}(X,y,\mathbf{w})+\lambda\,\mathcal{R}(\mathbf{w}) \end{align}\)
커널 알고리즘(Kernel Algorithm)은 데이터를 비선형 고차원 공간으로 매핑하는 알고리즘입니다. 이때의 목적 함수는 다음과 같습니다. \(\begin{align} \mathcal{L}(\mathbf{w})=\mathcal{L}\bigl(\phi(X),y,\mathbf{w}\bigr)+\lambda\,\mathcal{R}(\mathbf{w}) \end{align}\)
위 수식처럼 목적 함수가 커널 알고리즘이고 노름 정규화를 포함한다면, Representer theorem을 적용할 수 있습니다. Representer theorem에 따르면, 최적화된 모델 파라미터 w는 매핑결과들의 선형결합으로 표현됩니다. 따라서 커널 알고리즘일 때는 실제로 최적화해야 대상이 w에서 α로 대체됩니다. 그 결과, α도 w와 동등하게 모델 파라미터로 활용됩니다.
\[\begin{align} \mathbf{w} = \sum_i \alpha_i \phi(x_i) \end{align}\]| 목적 함수 | 모델 파라미터 | 예시 |
|---|---|---|
| 비커널 알고리즘 | \(\mathbf{w}\) | RR(Ridge Regression), LR(Logistic Regression), LASSO, SVM(Support Vector Machine) |
| 커널 알고리즘 | \(\mathbf{w},\ \boldsymbol{\alpha}\) | KLR(Kernel Logistic Regression), KSVM(Kernel Support Vector) |
해석적 해 vs 근사 해
해석적 해 (Analytical solution)는 수학적으로 직접 풀어서 구한 정확한 해를 의미합니다.
근사 해 (Approximate solution)는 경사하강법처럼 반복적 최적화를 통해 추정한 해를 의미합니다.
해석적 해는 반복적 시행착오를 거치지 않아도 되지만 계산이 복잡한 경우 적용하기 어렵고, 근사 해는 실용적이지만 오차를 동반할 수 있습니다.
Threat Model
공격 대상 알고리즘에는 Linear regression, Kernel regression, Linear classification, Kernel classification, Neural networks이 포함됩니다.
공격자는 학습 데이터셋, 학습 알고리즘, 그리고 모델 파라미터를 알고 있다고 가정합니다. 만약 모델 파라미터를 알 수 없다면, 기존 연구에서 제안된 모델 파라미터 도용 기술을 활용한다고 가정합니다.
하이퍼파라미터 λ 추정
공격자는 목적 함수의 기울기가 0일 때로 선형 방정식을 설정하고, 이를 만족시키는 하이퍼파라미터 λ를 계산합니다.
비커널 알고리즘 목적 함수
\[\begin{align} \frac{\partial \mathcal{L}_{\text{loss}}(X,\,y,\,\mathbf{w})}{\partial \mathbf{w}} \;+\; \lambda\,\frac{\partial \mathcal{R}(\mathbf{w})}{\partial \mathbf{w}} \;=\; 0 \end{align}\] \[\begin{align} \mathbf{b} \;=\; \begin{bmatrix} \dfrac{\partial \mathcal{L}(X,y,\mathbf{w})}{\partial w_1} \\ \dfrac{\partial \mathcal{L}(X,y,\mathbf{w})}{\partial w_2} \\ \vdots \\[2pt] \dfrac{\partial \mathcal{L}(X,y,\mathbf{w})}{\partial w_m} \end{bmatrix}, \qquad \mathbf{a} \;=\; \begin{bmatrix} \dfrac{\partial \mathcal{R}(\mathbf{w})}{\partial w_1} \\ \dfrac{\partial \mathcal{R}(\mathbf{w})}{\partial w_2} \\ \vdots \\[2pt] \dfrac{\partial \mathcal{R}(\mathbf{w})}{\partial w_m} \end{bmatrix} \end{align}\] \[\begin{align} \frac{\partial \mathcal{L}(\mathbf{w})}{\partial \mathbf{w}} \;=\; \mathbf{b} \;+\; \lambda\,\mathbf{a} \;=\; 0 \end{align}\]커널 알고리즘인 목적 함수
\[\begin{align} \frac{\partial \mathcal{L}_{\text{loss}}\bigl(\phi(\mathbf{X}),\,y,\,\mathbf{w}\bigr)} {\partial \boldsymbol{\alpha}} \;+\; \lambda\, \frac{\partial \mathcal{R}(\mathbf{w})} {\partial \boldsymbol{\alpha}} \;=\; 0 \end{align}\] \[\mathbf{b} \;=\; \begin{bmatrix} \dfrac{\partial \mathcal{L}\bigl(\phi(X),y,\mathbf{w}\bigr)}{\partial \alpha_1} \\ \dfrac{\partial \mathcal{L}\bigl(\phi(X),y,\mathbf{w}\bigr)}{\partial \alpha_2} \\ \vdots \\[2pt] \dfrac{\partial \mathcal{L}\bigl(\phi(X),y,\mathbf{w}\bigr)}{\partial \alpha_n} \end{bmatrix}, \qquad \mathbf{a} \;=\; \begin{bmatrix} \dfrac{\partial \mathcal{R}(\mathbf{w})}{\partial \alpha_1} \\ \dfrac{\partial \mathcal{R}(\mathbf{w})}{\partial \alpha_2} \\ \vdots \\[2pt] \dfrac{\partial \mathcal{R}(\mathbf{w})}{\partial \alpha_n} \end{bmatrix}\] \[\begin{align} \frac{\partial \mathcal{L}(\boldsymbol{\alpha})}{\partial \boldsymbol{\alpha}} \;=\; \mathbf{b} \;+\; \lambda\,\mathbf{a} \;=\; 0 \end{align}\]만약 λ의 개수보다 선형 방정식의 개수가 더 많은 경우(Over‑determined)라면, 정확한 λ를 계산하기 어렵습니다. 이런 경우, 가장 근사한 λ를 계산하기 위하여 최소자승법(Least-Squares solution)을 사용해 추정치를 계산합니다. \(\begin{align} \hat{\lambda} \;=\; -\,(\mathbf{a}^\top \mathbf{a})^{-1}\,\mathbf{a}^\top \mathbf{b} \end{align}\) 추정된 하이퍼파라미터에 대해서는 상대추정오차(Relative estimation error)를 지표삼아 공격자의 하이퍼파라미터 추정 성능을 평가합니다. 상대추정오차가 작을수록 실제 모델 성능에 가까워지므로, 공격 성능이 높아집니다.
| 기호 | 의미 |
|---|---|
| \(\lambda\) | 실제 하이퍼파라미터 |
| \(\hat{\lambda}\) | 공격자가 추정한 하이퍼파라미터 |
| \(\Delta\hat{\lambda}\) | \(\hat{\lambda}-\lambda\) |
| \(\mathbf{w},\ \boldsymbol{\alpha}\) | 실제로 학습된 / 도용된 모델 파라미터 |
| \(\boldsymbol{\mathbf{w}}^{\star},\ \boldsymbol{\alpha}^{\star}\) | 목적 함수가 이론적으로 최소화되었을 때 도달하는 정확한 최소값에 해당하는 파라미터 |
| \(\Delta\mathbf{w},\ \Delta\boldsymbol{\alpha}\) | \(\mathbf{w}-\mathbf{w}^{\star},\ \boldsymbol{\alpha}-\boldsymbol{\alpha}^{\star}\) |
| \(\epsilon\) | \(\frac{\lvert \hat{\lambda}-\lambda \rvert}{\lambda}\) |
\(\begin{align} Relative \ estimation \ error: \epsilon \;=\; \frac{\lvert \hat{\lambda}-\lambda \rvert}{\lambda} \end{align}\) 학습된 모델 파라미터가 목적 함수의 실제 최소지점과 근접할수록, 하이퍼파라미터의 추정오차에 대한 상한선이 아래 수식과 같이 성립합니다. 이는 하이퍼파라미터 추정오차가 너무 커지지 않고 예측 가능한 범위 안에 든다는 의미입니다. \(\begin{align} \Delta\hat{\lambda} &= \hat{\lambda}-\lambda = \Delta\mathbf{w}^{\top}\, \nabla\hat{\lambda}\!\bigl(\mathbf{w}^{\star}\bigr) + O\!\bigl(\Delta\mathbf{w}\rVert_{2}^{2}\bigr) &\quad (\Delta\mathbf{w}\to 0) \\[4pt] \end{align}\)
\(\begin{align} \Delta\hat{\lambda} &= \hat{\lambda}-\lambda = \Delta\boldsymbol{\alpha}^{\top}\, \nabla\hat{\lambda}\!\bigl(\boldsymbol{\alpha}^{\star}\bigr) + O\!\bigl(\Delta\boldsymbol{\alpha}\rVert_{2}^{2}\bigr) &\quad (\Delta\boldsymbol{\alpha}\to 0) \end{align}\)
MLaaS에서 하이퍼파라미터 도용 방법
머신러닝은 기본적으로 아래의 과정을 따릅니다.
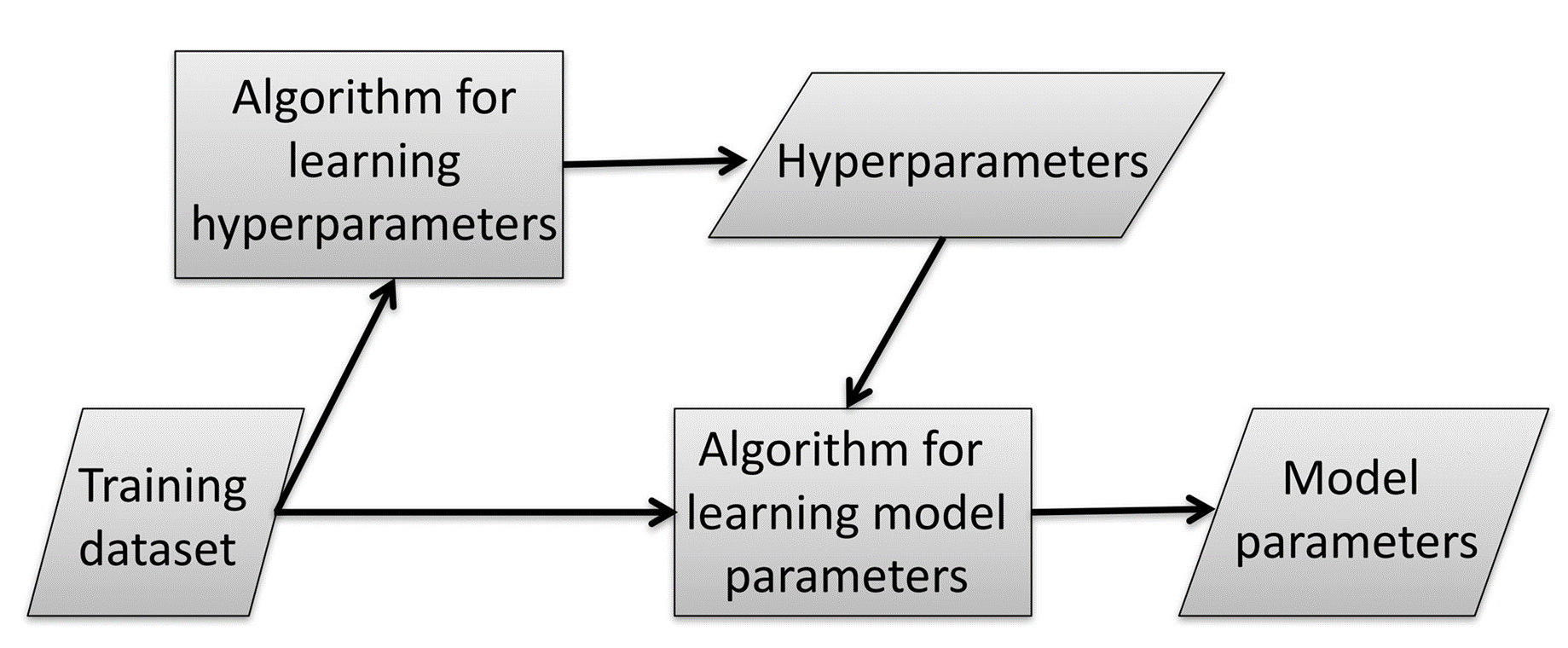
공격자는 이 과정 속에서 두 가지 Protocol을 활용해 하이퍼파라미터를 도용합니다.
Protocol 1: 사용자가 전체 학습 데이터셋과 학습 알고리즘을 MLaaS 플랫폼에 업로드하면, MLaaS는 하이퍼파라미터와 모델 파라미터를 학습한 뒤 모델 파라미터를 반환합니다.
Protocol 2: 사용자가 전체 학습 데이터셋과 학습 알고리즘, 하이퍼파라미터를 MLaaS 플랫폼에 업로드하면, MLaaS는 모델 파라미터를 학습합니다.
공격자는 이 Protocol을 다음과 같은 방식으로 활용합니다. 먼저, 공격자는 학습 데이터셋 일부만 Protocol 1에 적용해 모델 파라미터를 얻고, MLaaS가 학습한 하이퍼파라미터를 추정합니다. 그 다음, 데이터셋 전체와 추정한 하이퍼파라미터를 Protocol 2에 적용해 저비용으로 고성능 모델을 학습합니다. 이 과정에서 공격자는 고비용의 하이퍼파라미터 학습 단계를 우회할 수 있습니다.
본 논문은 이 과정을 Train-Steal-Retrain 전략으로 부르며, 이를 MLaaS 플랫폼의 비용 구조를 악용하는 방식으로 설명합니다.
방어 방법
본 논문에서 제안하는 MLaaS에서의 하이퍼파라미터 도용 방어 기법은 다음과 같습니다.
MLaaS는 Protocol 1에서 학습한 모델 파라미터를 사용자에게 반환할 때 반올림된 값을 제공합니다. 이 방법은 공격자의 하이퍼파라미터 추정 오류를 늘려 도용 성능을 효과적으로 저하시킵니다.
Experiment
아래 실험은 여러 목적 함수의 하이퍼파라미터를 추정하고, 실제 하이퍼파라미터와의 상대추정오차를 분석합니다.
또한, 실제 MLaaS 플랫폼에서 하이퍼파라미터 추정 성능을 평가합니다.
마지막으로, 반올림 기반 방어법의 성능과 한계도 살펴봅니다.
학습 데이터셋
| 이름 | 샘플 수 | 차원 | 유형 | 내용 |
|---|---|---|---|---|
| Diabetes | 442 | 10 | Regression | 질병 진행 예측 |
| GeoOrig | 1059 | 68 | Regression | 지리적 변수 예측 |
| UJIIndoor | 19937 | 529 | Regression | 실내 위치 예측 |
| Iris | 100 | 4 | Classification | 붓꽃 분류 |
| Madelon | 4400 | 500 | Classification | 이진 분류 |
| Bank | 45210 | 16 | Classification | 정기예금 가입 예측 |
실험결과
Regression
| 목적 함수 | 손실 함수 | 정규화 |
|---|---|---|
| RR | Least square | L2 |
| LASSO | Least square | L1 |
| KRR | Least square | L2 |
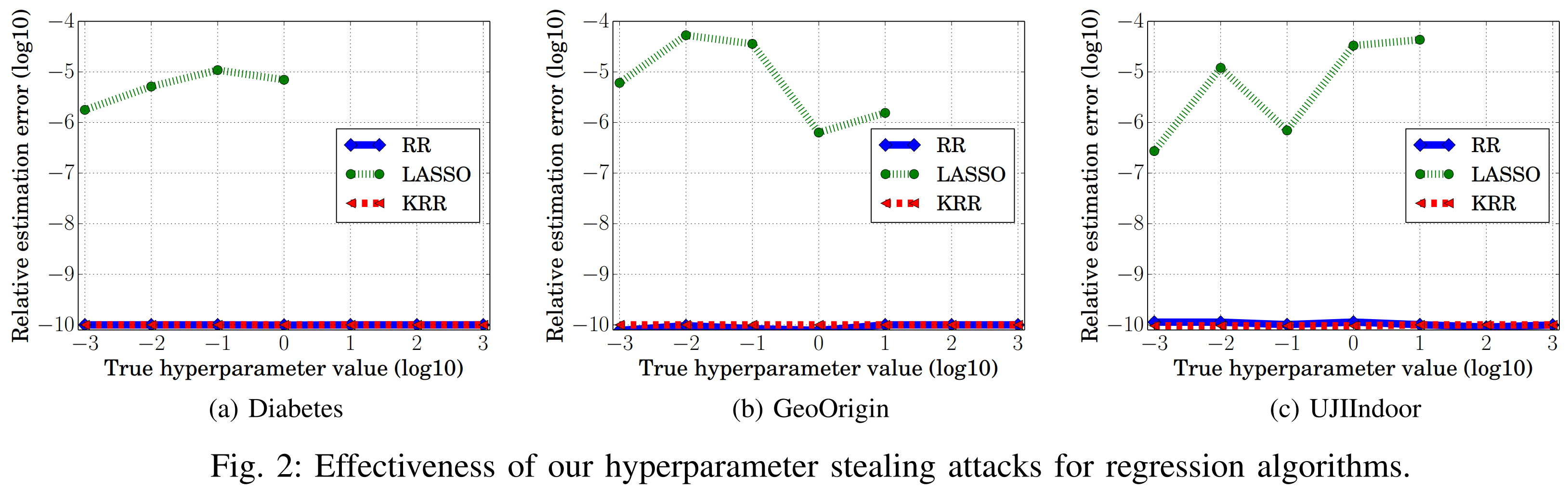
위 그래프를 보면, 목적함수가 RR, KRR일 때 상대추정오차가 매우 작습니다. 이는 두 목적 함수가 학습한 모델 파라미터가 해석적 해(Analytical solutions)를 따르기 때문입니다. 그 결과, RR과 KRR의 모델 파라미터 w와 α는 목적함수의 정확한 최소지점에 도달한 결과와 일치합니다. 다시 말해, ∆w, ∆α = 0이라서 하이퍼파라미터 추정오차가 0이 되고, 완벽한 하이퍼파라미터 도용이 이루어집니다.
반면 다른 목적 함수들은 모델 파라미터에 대한 해석적 해가 없기 때문에 ∆w 또는 ∆α가 0이 아닐 가능성이 높습니다. 이런 목적 함수들에서는 상대추정오차가 비교적 크게 나타나는 모습을 보입니다.
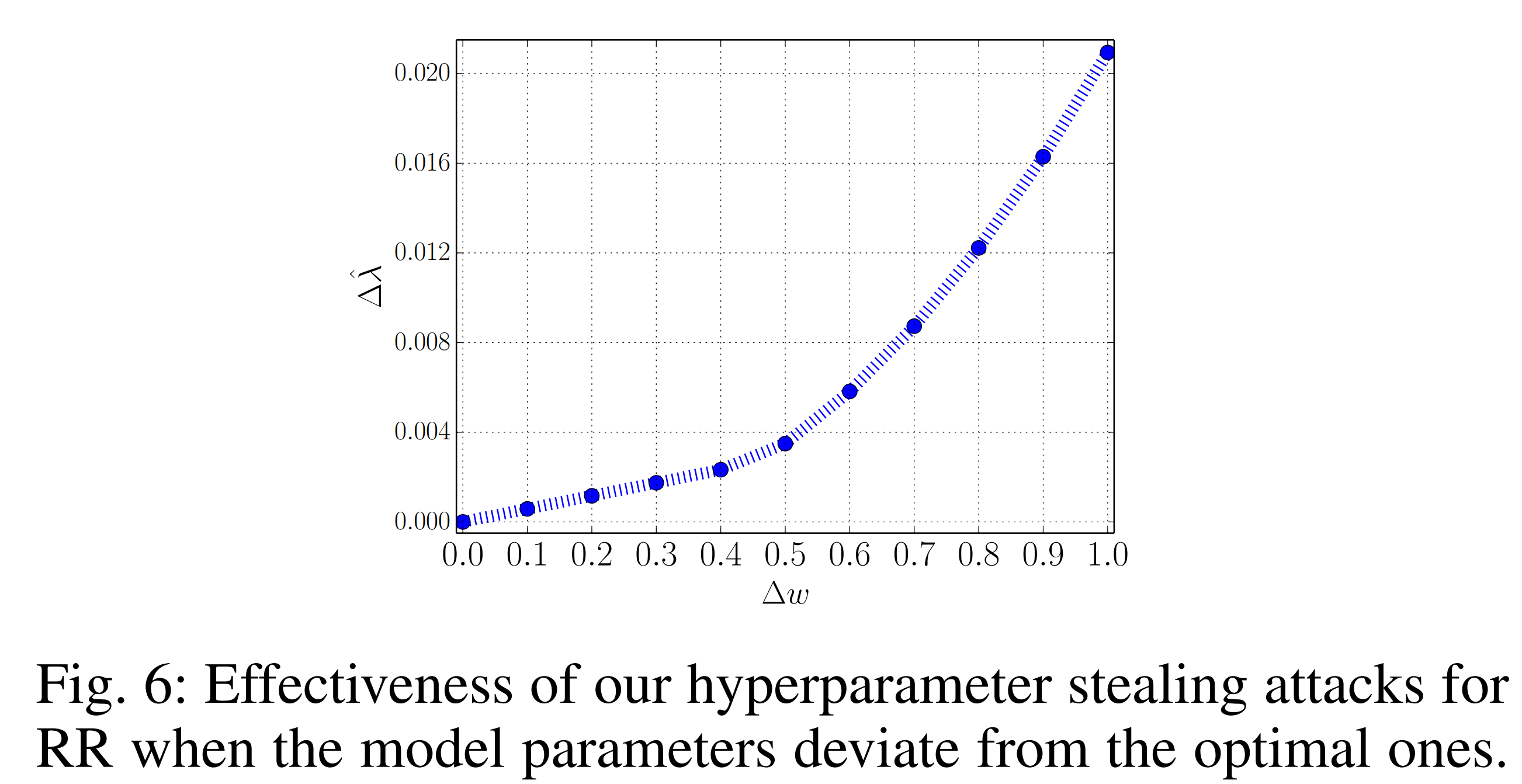
아래 그래프는 RR의 모델 파라미터가 근사 해(Approximate solutions)를 따르게 한 결과입니다. ∆w에 따른 하이퍼파라미터 추정오차의 변화를 분석한 결과, ∆w가 작을 때는 선형적으로 증가하는 경향을 보였지만, 그 이후부터는 비선형적인 증가 패턴이 나타났습니다. 이러한 양상은 하이퍼파라미터 추정오차가 선형 항과 비선형 항의 합으로 이루어져 있다는 점에서 자연스럽게 설명됩니다.
Logistic Regression
| 목적 함수 | 손실 함수 | 정규화 |
|---|---|---|
| L2-LR | Cross Entropy | L2 |
| L1-LR | Cross Entropy | L1 |
| L2-KLR | Cross Entropy | L2 |
| L1-KLR | Cross Entropy | L1 |
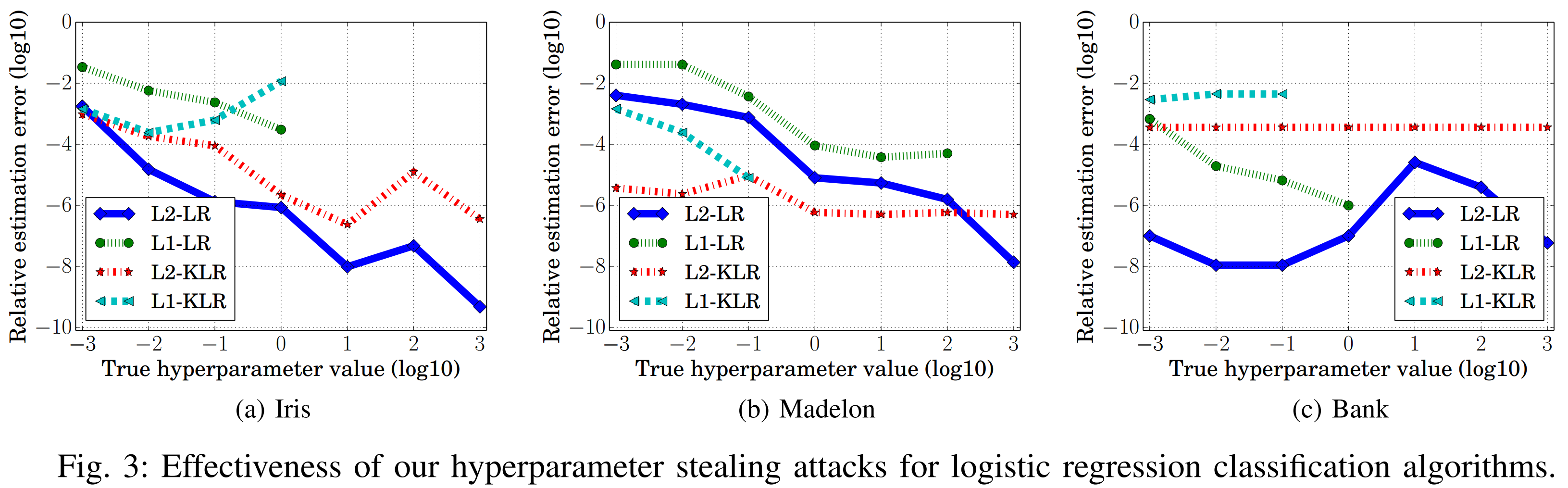
위 그래프를 보면, 목적 함수가 L2 정규화를 사용했을 때 L1 정규화에 비해 상대추정오차가 비교적 작습니다. L2 정규화의 미분값은 2w로써, 학습을 연속적으로 조정하여 목적 함수가 최소값에 안정적으로 다가가게 합니다. 이는 상대추정오차를 줄이는 데 기여하며, 결과적으로 하이퍼파라미터 도용 공격의 성능을 증가시킵니다.
반면, L1 정규화의 미분값 sign(w)는 학습을 불연속적으로 조정해 상대추정오차가 커질 가능성이 높으며, 이에 따라 도용 공격의 성능이 낮아질 수 있습니다.
MLaaS 실험결과
본 연구는 MLaaS 플랫폼을 대상으로 세 가지 방법(M1, M2, M3)을 설정하고, 각 방법대로 학습한 결과를 비교분석합니다.
M1: Protocol 1 진행
M2: 학습 데이터셋 일부만으로 Protocol 1 진행
M3: 학습 데이터셋 일부만으로 Protocol 1진행 → 하이퍼파라미터 추정 → Protocl 2 진행
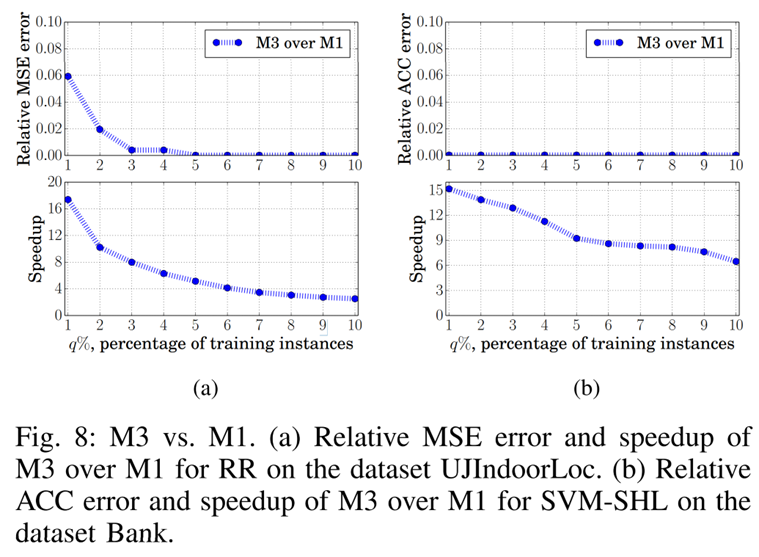
위 그래프를 보면 M3과 M1 사이의 Relative MSE error, Relative ACC error가 매우 작습니다. 이를 통해 M1의 성능과 하이퍼파라미터를 도용한 M3의 성능이 비슷하다고 해석할 수 있습니다.
심지어 속도 측면에서는 M3가 M1에 비해 더 높은 성능을 보입니다.
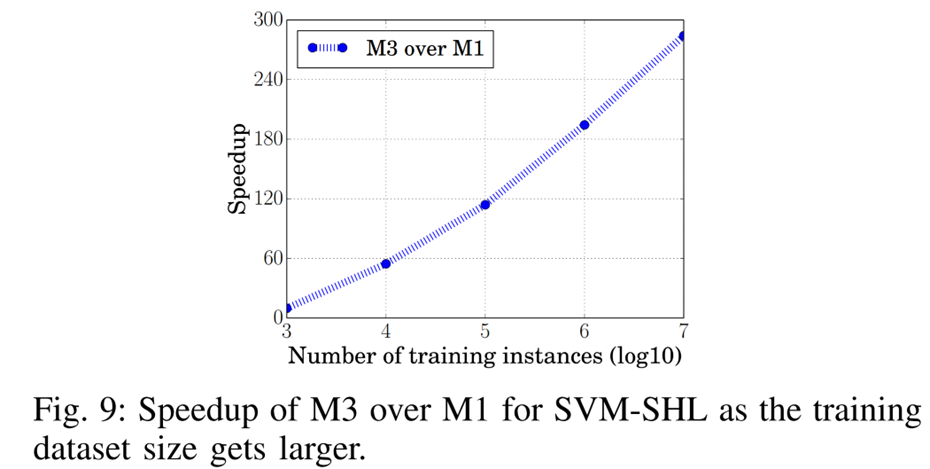
위 그래프를 통해 훈련 데이터셋의 크기가 커질수록 M3의 학습 속도가 높아짐을 알 수 있습니다.
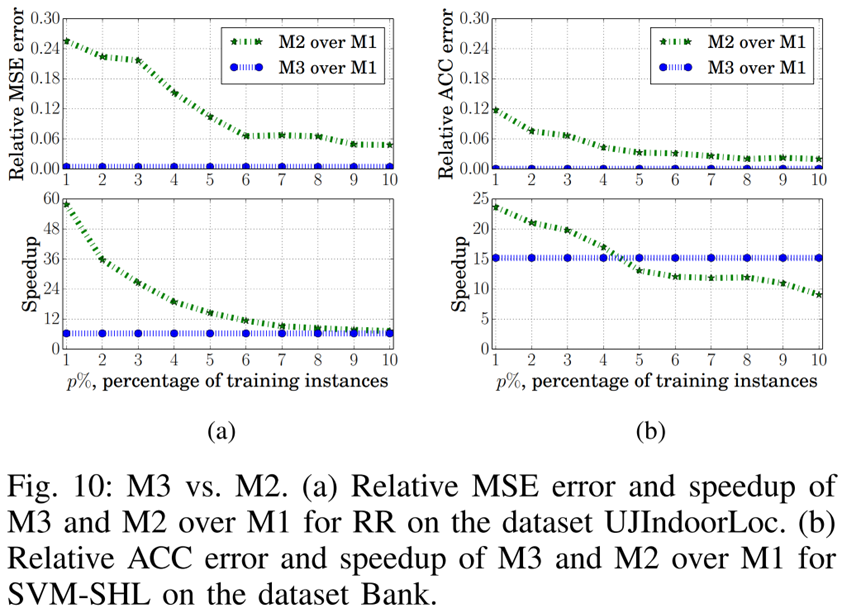
위 그래프를 통해 다음 사실을 알 수 있습니다. M3와 M2는 둘 다 Protocol 1에서 학습 데이터셋의 일부만 활용하지만, M3는 데이터 비율을 줄여도 M2보다 더 높은 성능을 발휘합니다.
하이퍼파라미터 도용 공격에 대한 방어 실험
평가 지표
만약 아래 지표들이 높게 나타난다면, 반올림 기반 방어의 성능이 뛰어나다고 볼 수 있습니다. \(\begin{align} Relative \ estimation \ error: \dfrac{|\hat{\lambda}_{\text{after Rounding}} -\lambda_{\text{before Rounding}}|}{\lambda_{\text{before Rounding}}} \end{align}\)
\[\begin{align} Relative \ MSE \ error: \dfrac{|\text{MSE}_{\text{after Rounding}} -\text{MSE}_{\text{before Rounding}}|}{\text{MSE}_{\text{before Rounding}}} \end{align}\] \[\begin{align} Relative \ ACC \ error: \dfrac{|\text{ACC}_{\text{after Rounding}} -\text{ACC}_{\text{before Rounding}}|}{\text{ACC}_{\text{before Rounding}}} \end{align}\]실험결과
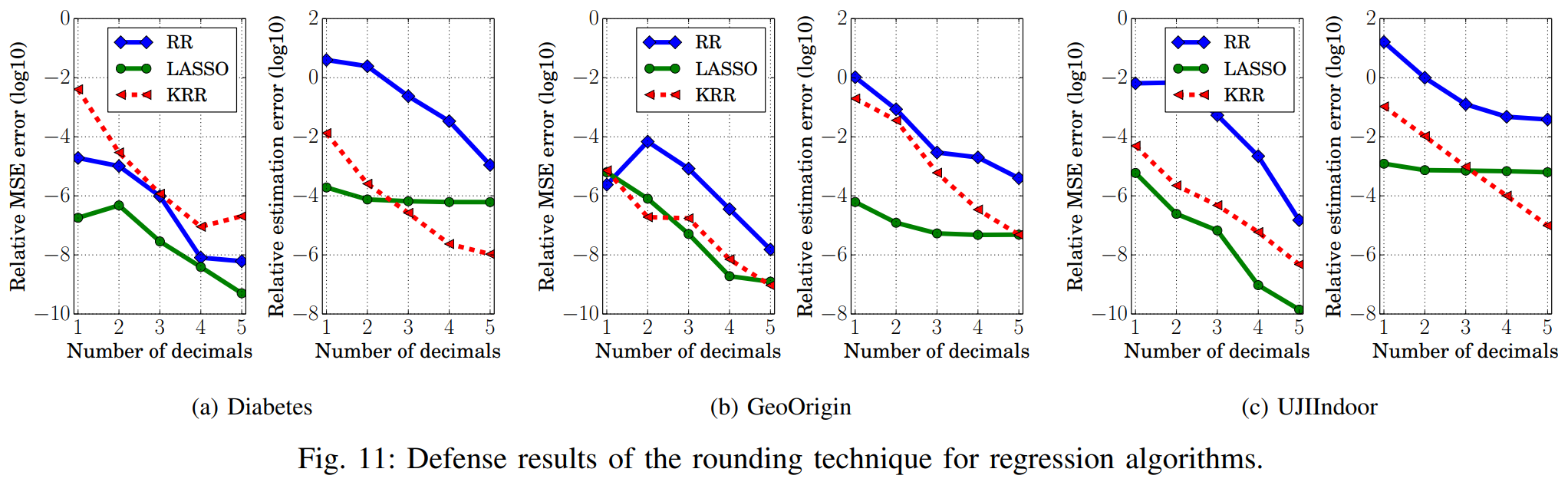
위 그래프를 보면, 대부분의 목적 함수는 반올림 이후 상대추정오차가 높지만, LASSO는 반올림을 적용하더라도 상대추정오차가 여전히 낮은 모습을 보입니다. 이를 통해 반올림 방어법이 LASSO에 대한 하이퍼파라미터 도용 공격은 방어하지 못 함을 알 수 있습니다.
그리고 반올림하는 모델 파라미터의 소수점 자릿수(Number of decimals)를 늘릴수록, 반올림 방어의 성능이 약화되는 경향을 보입니다. 따라서 소수점 자릿수가 낮은 구간에서의 결과를 분석에 유의미하다고 해석할 수 있습니다.
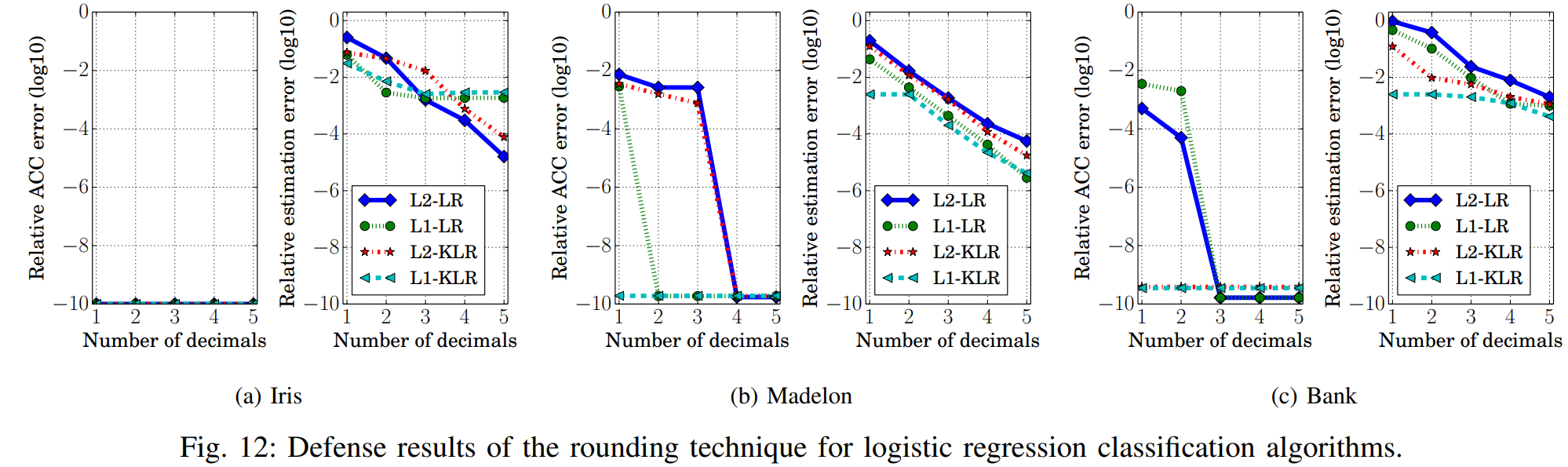
위 그래프를 보면 소수점 자릿수가 낮을 때, L2 정규화를 사용하는 목적 함수가 L1 정규화를 사용하는 목적 함수보다 평가지표들이 높습니다. 즉, L2 정규화를 사용할 때 하이퍼파라미터 도용 공격에 대한 방어 성능이 더 좋다는 의미로 해석할 수 있습니다. L2 정규화는 L1 정규화와 달리 미분값이 연속적이어서, 반올림에 따른 변화가 그대로 반영됩니다. 그로 인해 하이퍼파라미터 상대추정오차가 더 효과적으로 커지며, 도용 공격 성공 가능성을 더 잘 낮출 수 있습니다.
MLaaS 실험결과
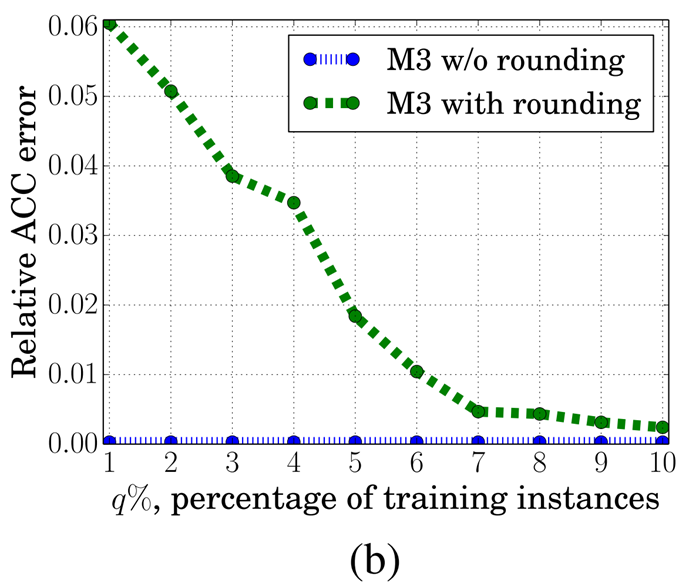
아래 그래프는 MLaaS의 M3 방법에서 반올림 여부를 비교한 결과를 보여줍니다. 이때 반올림 방어를 적용했을 때 평가지표가 더 높은 경향을 보이며, 이는 반올림 방어가 MLaaS 환경에서도 효과적임을 보여줍니다.
결론
본 연구는 하이퍼파라미터 도용 공격이 MLaaS 환경에서 학습 비용을 절감하면서도 모델 성능을 유지할 수 있음을 실험을 통해 확인했습니다. 반올림 방어 기법은 L2 정규화를 사용하는 알고리즘에서 추정 오차를 효과적으로 늘려 공격 성공 가능성을 감소시킵니다. 다만, 일부 알고리즘에서는 추정 오차가 여전히 작게 유지되어 새로운 대응책의 필요성이 드러났습니다.
따라서 앞으로 다양한 하이퍼파라미터 유형에 대한 도용 공격과 이를 방어할 수 있는 새로운 연구가 필요할 것으로 보입니다.