[NeurIPS🎉] Unlearning-Aware Minimization

• Introduction
• Preliminary
  • Machine Unlearning Problem
  • Existing Approximate Unlearning Methods
• Main Results
  • Efficient Algorithm via First-Order Approximation
  • Theoretical Insights
  • Performance on Image Classification Unlearning
  • Performance on LLM Unlearning
• Conclusion
• Implementation
  • Related Papers from the Lab

Introduction

In today’s AI-driven world, protecting user privacy has become paramount. The “right to be forgotten”, enshrined in regulations like GDPR, grants individuals the power to request deletion of their personal data. But what happens when AI models have already been trained on this data?

Machine unlearning addresses “Can we make an AI model forget specific training data without retraining from scratch?” This is crucial not only for privacy compliance but also for removing poisoned data, correcting training mistakes, and ensuring trustworthy AI systems.

“Unlearning-Aware Minimization (UAM)” [Paper] is a paper from our lab that introduces a novel min-max optimization framework for machine unlearning. This article will explore both the concept of machine unlearning and our proposed method.

Preliminary

Machine Unlearning Problem

To understand machine unlearning, we first need to understand what a model should achieve after “forgetting.” Given a training dataset \(\mathcal{D}\), we can partition it into two disjoint sets:

• Forget data \(\mathcal{D}_f\): The data we want the model to forget
• Retain data \(\mathcal{D}_r\): The data we want the model to remember

The ideal solution, called exact unlearning, is to retrain the model from scratch using only the retain data:

where \(\mathcal{L}(w, \mathcal{D})\) represents the loss function and \(w\) denotes the model parameters.

However, retraining is computationally prohibitive for large-scale models. For instance, retraining a ResNet model on CIFAR-10 takes over 30 minutes, while large language models can require days or weeks. This has led to the development of approximate unlearning methods that efficiently update pre-trained model parameters.

Existing Approximate Unlearning Methods

Prior research has proposed two main approaches to approximate unlearning:

1. Fine-Tuning (FT): Simply continues training on the retain data only \(\begin{equation} \min_w \mathcal{L}(w, \mathcal{D}_r) \end{equation}\)

2. Negative Gradient (NG): Maximizes loss on the forget data to unlearn \(\begin{equation} \max_w \mathcal{L}(w, \mathcal{D}_f) \end{equation}\)

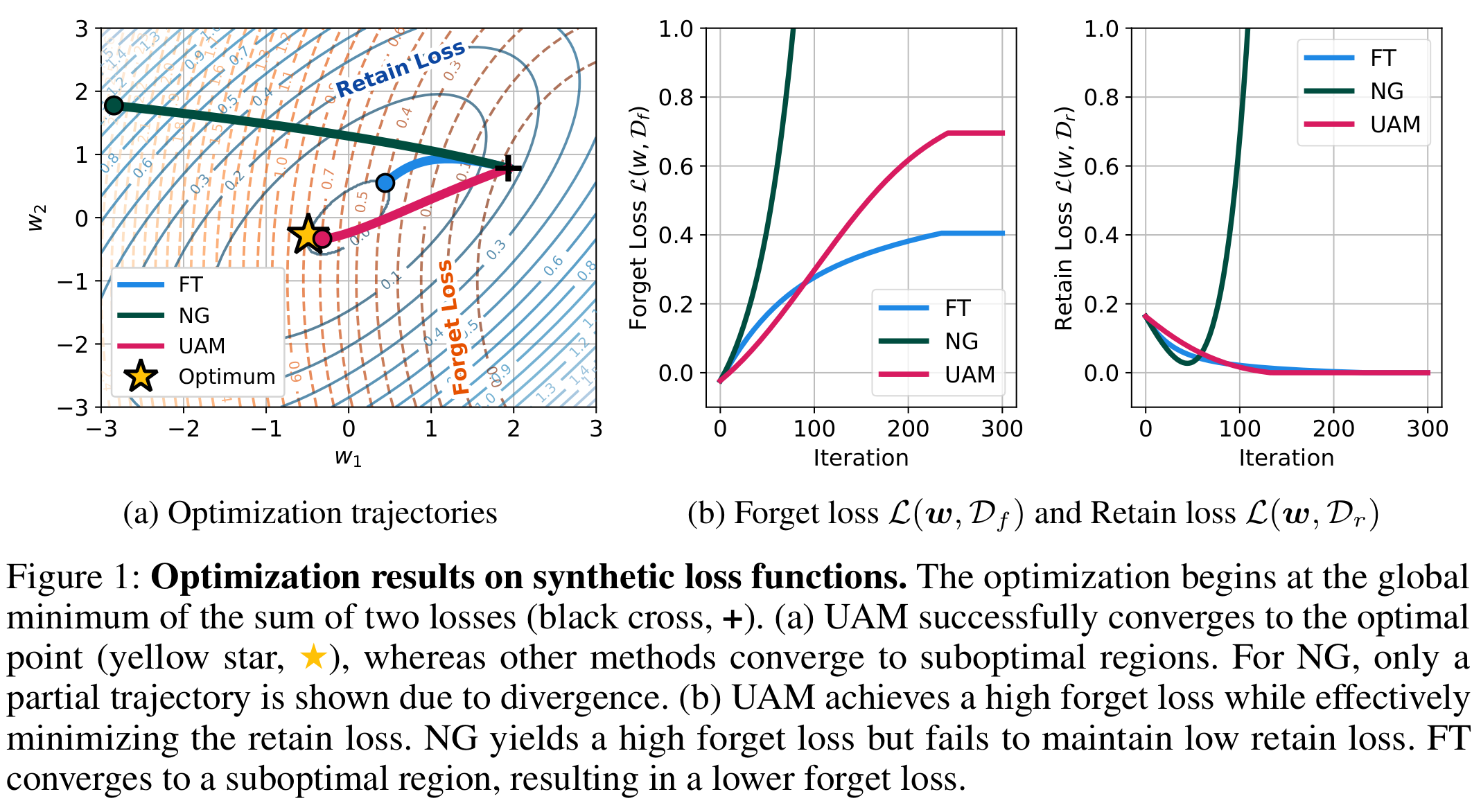
While FT maintains good performance on retain data, it often fails to sufficiently remove the influence of forget data. On the other hand, NG successfully removes forget data but severely degrades performance on retain data. Both methods converge to suboptimal solutions.

Main Results

This paper addresses the fundamental question: “How can we effectively forget specific data while maintaining performance on the retain data?” We propose Unlearning-Aware Minimization (UAM), a novel min-max optimization framework.

To understand the motivation behind UAM, we first establish a unified objective that characterizes existing approximate unlearning methods. Given that the optimal solution \(w^*\) lies within a bounded neighborhood of the pre-trained model, we can formulate the unlearning problem as:

This unified objective has two components:

1. Performance term: \(\mathcal{L}(w, \mathcal{D}_r)\) encourages the model to maintain performance on retain data
2. Consistency term: \(\mathcal{L}(w^*, \mathcal{D}) - \mathcal{L}(w, \mathcal{D})\) encourages alignment between the optimized weights and the optimal solution

This framework explains two main approaches to approximate unlearning:

• Fine-Tuning (FT): Sets \(\beta = 0\), ignoring the consistency term and resulting in poor forgetting
• Negative Gradient (NG): Assumes no knowledge on \(w^*\), focuses solely on maximizing forget loss, struggling to maintain retain performance

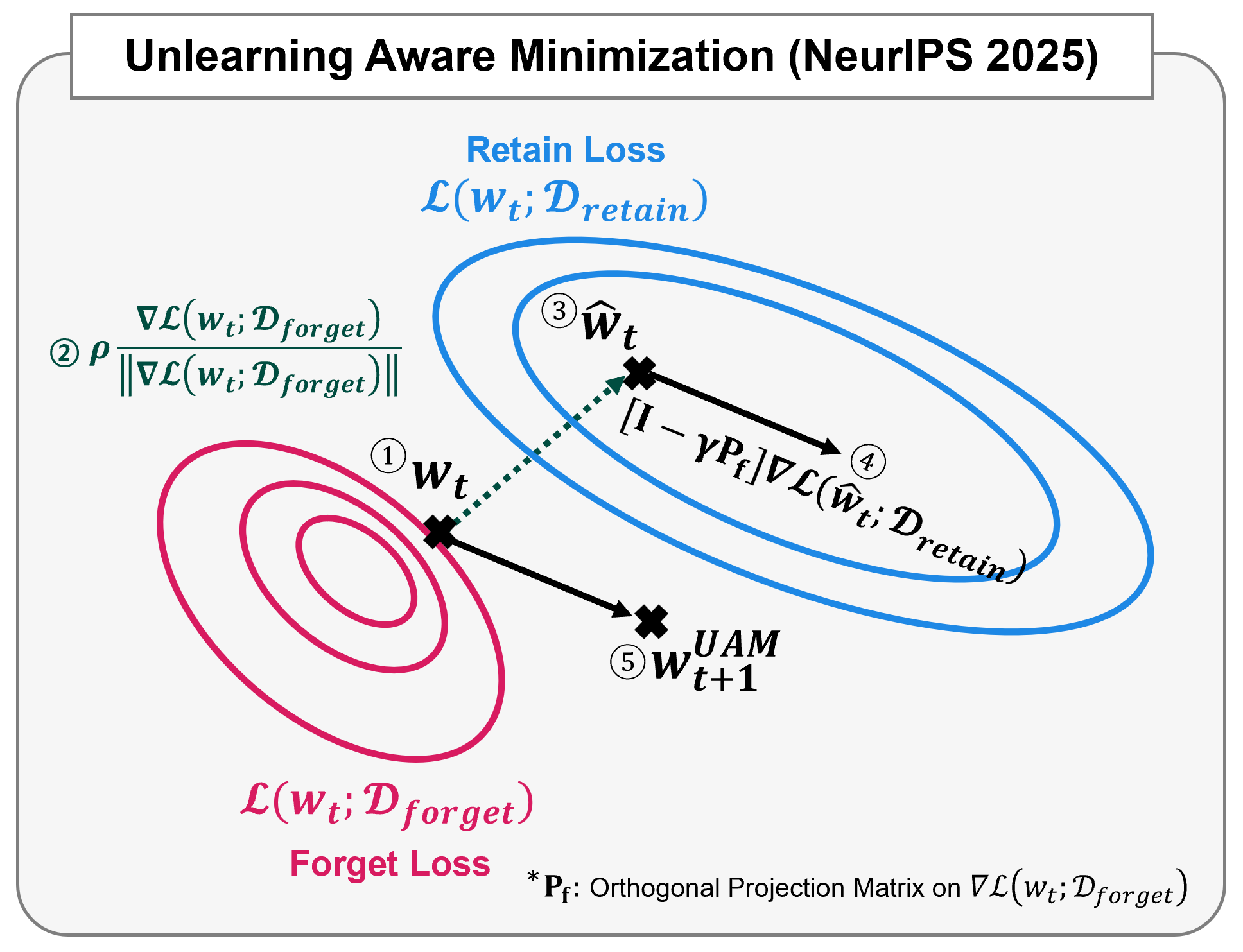
The key insight of UAM is to leverage parameters with high forget loss to guide the unlearning process. We formulate this as:

This min-max formulation has two stages:

1. Inner maximization: Find perturbed parameters \(\hat{w}=\text{argmax}_{\|\delta\|_2 \leq \rho} \mathcal{L}(w + \delta, \mathcal{D}_f)\) that maximize forget loss
2. Outer minimization: Update parameters with gradients that minimize retain loss at \(\hat{w}\)

By using parameters with high forget loss as a reference point, UAM ensures that the updated model exhibits high-forget-loss characteristics while maintaining low retain loss.

Efficient Algorithm via First-Order Approximation

Computing the exact solution to the inner maximization problem is computationally expensive. We apply a first-order Taylor approximation to derive an efficient algorithm:

This formulation can be efficiently implemented using automatic differentiation frameworks like PyTorch. A key advantage of UAM is its framework-agnostic nature. UAM can be easily integrated with other unlearning methods.

Theoretical Insights

Our theoretical analysis reveals that the gradient of UAM’s objective can be expressed as:

where \(\mathbf{P}_f\) is the orthogonal projection matrix onto the forget gradient direction, and \(\mathbf{H}_f\) is the Hessian of the forget loss.

The key insight is the term \((\mathbf{I} - 2\mathbf{P}_f)\), which subtracts twice the component of the retain gradient aligned with the forget gradient. This mathematical operation ensures that the update direction moves away from directions that would decrease the forget loss.

Computing the exact Hessian matrix \(\mathbf{H}_f\) is computationally expensive. We find that approximating the Hessian with the identity matrix yields a simple yet effective solution:

where \(\gamma\) is a hyperparameter. In practice, we find that \(\gamma=2\) consistently achieves strong performance across various tasks with minimal additional computational cost.

A deeper analysis reveals the geometric intuition behind UAM. Applying first-order approximation to our objective yields:

This shows that UAM explicitly minimizes the inner product (cosine similarity) between the retain gradient \(\nabla \mathcal{L}(w, \mathcal{D}_r)\) and the forget gradient \(\nabla \mathcal{L}(w, \mathcal{D}_f)\).

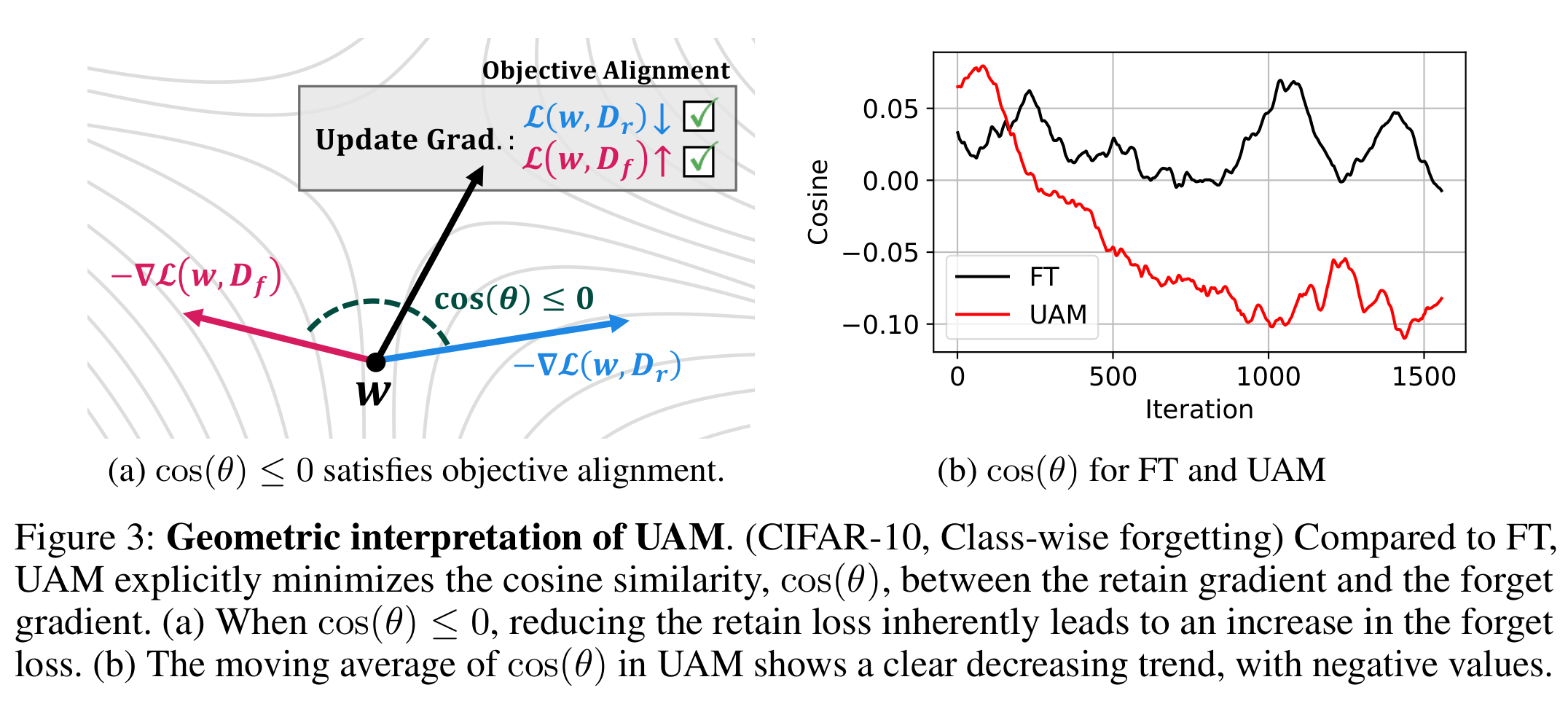
When these gradients become negatively aligned (cosine similarity ≤ 0), minimizing the retain loss inherently leads to maximizing the forget loss. This provides a powerful geometric explanation for why UAM outperforms existing methods.

Performance on Image Classification Unlearning

We evaluate UAM on three benchmark datasets: CIFAR-10, CIFAR-100, and TinyImageNet, under two scenarios:

• Class-wise forgetting: Remove all samples from a specific class
• Random data forgetting: Remove randomly sampled training examples

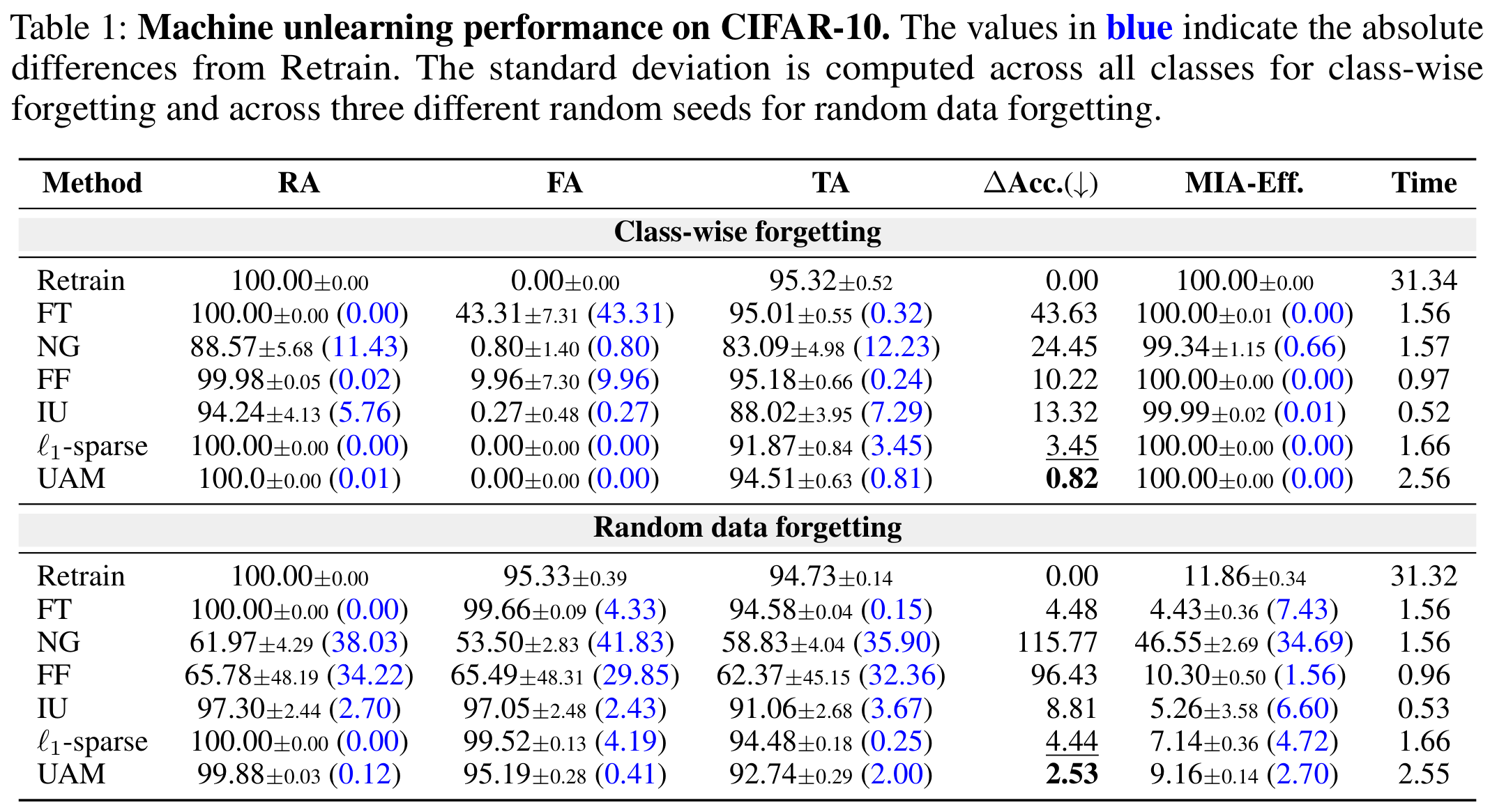
Key findings:

• UAM achieves zero forget accuracy on class-wise forgetting, matching exact retraining
• NG diverges under random forgetting, while UAM remains stable
• UAM outperforms all baselines with the lowest \(\Delta\)Acc. metric

Performance on LLM Unlearning

Beyond vision tasks, UAM demonstrates remarkable effectiveness in making large language models (LLMs) forget hazardous knowledge. For Zephyr-7B-β, UAM achieves the lowest hazardous knowledge scores on WMDP-Bio and WMDP-Cyber.

When prompted with a hazardous question about engineering a more virulent strain of influenza, the base model provides detailed dangerous information. After unlearning with UAM, the model appropriately refuses to provide such hazardous content, ensuring safer behavior.

Conclusion

Machine unlearning is essential for building trustworthy AI systems that respect user privacy and comply with data protection regulations. The challenge lies in effectively removing the influence of specific data while maintaining model performance—a task that existing methods struggle with.

Unlearning-Aware Minimization (UAM) introduces a principled min-max optimization framework that:

• Effectively removes forget data with near-zero forget accuracy
• Works across domains from image classification to large language models
• Provides theoretical insights through gradient alignment analysis

Our experiments demonstrate that UAM outperforms existing methods on multiple benchmarks, including CIFAR-10, CIFAR-100, TinyImageNet, and WMDP. By explicitly leveraging the geometry of the loss landscape and the relationship between retain and forget gradients, UAM discovers better solutions that prior methods fail to reach.

The field of machine unlearning still has many open challenges, from theoretical guarantees to more efficient algorithms. We hope that UAM contributes to the development of privacy-preserving AI systems that can adapt to evolving data requirements while maintaining high performance.

Implementation

We release our implementation as an open-source package: machine-unlearning-pytorch

import torchunlearn
from torchunlearn.unlearn.trainers.uam import UAM

# Load pre-trained model
model = torchunlearn.utils.load_model(model_name="ResNet18", n_classes=10)
rmodel = torchunlearn.RobModel(model, n_classes=10)

# Setup UAM trainer
trainer = UAM(rmodel, rho=0.01, gamma=2.0)

# Configure optimization
trainer.setup(
    optimizer="SGD(lr=0.01, momentum=0.9, weight_decay=5e-4)",
    scheduler=None,
    n_epochs=5
)

# Train with unlearning
trainer.fit(
    train_loaders=merged_loader,  # Contains both retain and forget data
    n_epochs=5,
    save_path="./models/unlearned",
    save_best={"Clean(R)": "HB", "Clean(F)": "LBO"}
)

Check out our repository at: [GitHub]

Related Papers from the Lab

• Fantastic Robustness Measures: The Secrets of Robust Generalization [NeurIPS 2023] | [Paper] | [Article]
• Stability Analysis of Sharpness-Aware Minimization [arXiv 2023] | [Paper] | [Article]
• Differentially Private Sharpness-Aware Training [ICML 2023] | [Paper] | [Code]